Prova de que um conjunto é quociente se e só se é uma partição

Esta nota é para provar que todo conjunto quociente é uma partição e toda partição é um conjunto quociente.

Caso você não conheça essas (e outras) definições que falarei sobre, pode encontrá-las em:

Definições de Teoria de Conjuntos – Quarto 707

(quando eu for usar as definições ao longo do texto, linkarei esse post novamente)

Sumário

Prova de que toda partição é um conjunto quociente
Prova de que todo conjunto quociente é uma partição
Conclusão
Referências

Prova de que toda partição é um conjunto quociente

Comecemos provando que toda partição é um conjunto quociente. De forma mais precisa, o que vamos provar é:

Proposição

Seja $\mathbb{P}$ uma partição arbritária de um conjunto $A$ . Então $\mathbb{P}$ induz/define uma relação de equivalência $\sim$ . E mais, o conjunto quociente $A \setminus\sim \,$ desta relação de equivalência $\sim$ é a própria partição $\mathbb{P}$ que induziu a relação.

Prova

Sejam $x, y, z \in A$ elementos arbritários de $A$ e $\mathbb{P}$ uma partição de $A$ .

Vamos definir a seguinte relação $\sim$ induzida pela partição arbitrária $\mathbb{P}$ em $A$ :

$x \sim y \sse \exists B_i \in \mathbb{P}$ tal que $x, y \in B_i$ para algum $i$ .

Ou seja, dois elementos de $A$ estão relacionados se eles pertencem a mesma “parte” de $A$ .

O próximo passo é provar que essa relação é uma relação de equivalência. Então, pela definição de relação de equivalência, devemos mostrar que $\sim$ é reflexiva, simétrica e transitiva. Bora lá:

Reflexividade: Seja $x \in A$ . Pela definição de partição, $A = \bigcup\limits_{B_i \in \mathbb{P}} B_i$ , então temos que $x \in \bigcup\limits_{B_i \in \mathbb{P}} B_i$ , o que implica que $\exists i \in \mathbb{N}$ tal que $x \in B_i$ . Logo $x \sim x,$ , pois existe $\exists B_i \in \mathbb{P}$ tal que $x, x \in B_i$ .

Simetria: Seja $x, y \in A$ . Suponha que $x \sim y$ . Então temos por hipótese que $\exists B_i \in \mathbb{P}$ tal que $x, y \in B_i$ . Logo, $y \sim x$ , pois $y, x \in B_i$ .

Transitividade: Seja $x, y, z \in A$ . Suponha que $x \sim y$ e $y \sim z$ . Então $\exists B_1 \in \mathbb{P}$ tal que $x, y \in B_1$ e $\exists B_2 \in \mathbb{P}$ tal que $y, z \in B_2$ . Daí temos que $y \in B_1 \cap B_2$ , o que implica que $B_1 \cap B_2 \neq \emptyset$ , e portanto $B_1 = B_2$ (pela nossa definição de partição). Logo, $x, z \in B_1$ (ou $B_2$ , se prerferir). Daí decorre que $x \sim z$ (pela definição da nossa relação induzida por uma partição).

Provamos então que a relação $\sim$ induzida pela partição $\mathbb{P}$ é de fato uma relação de equivalência.

Ainda falta provar que o conjunto $A \setminus \sim$ de todas as classes de equivalências de $\sim$ é a própria partição $\mathbb{P}$ que induziu a relação de equivalência $\sim$ , mas isso deixo como exercício para você e o futuro André. Então, se você está lendo isso, saiba que ainda não fiz esse exercício, pois se tivesse feito teria atualizado esse texto.

Prova de que todo conjunto quociente é uma partição

Apesar de não termos terminado a prova de que toda partição é um conjunto quociente, continuemos.

Vamos agora provar que o conjunto de todas as classes de equivalência determinado por uma relação de equivalência arbitrária é ele próprio uma partição.

Mas antes disso, precisamos provar o seguinte lema:

Lema

Seja $A$ um conjunto não vazio, $x, y$ elementos arbitrários de $A$ , $\sim$ uma relação de equivalência arbitrária em $A$ e $\bar{x}=\{y \in A / x \sim y\}$ . Então $\bar{x} = \bar{y} \sse x \sim y$ .

Este lema nos diz que as classes de equivalência de $x$ e $y$ são a mesma classe se, e somente se, $x$ está relacionado com $y$ .

Prova do lema

(Ida) Suponha que $\bar{x}=\bar{y}$ . Temos que $\bar{x} \neq \emptyset$ pois toda relação de equivalência é reflexiva, então ao menos $x \in \bar{x}$ . Mas pela hipótese temos que $x \in \bar{x} \imp x \in \bar{y}$ , portanto $x \in \bar{y}$ , e daí decorre que $y \sim x$ . Então, pela simetria das relações de equivalência, $x \sim y$ , que era o que queríamos demonstrar.

(Volta) Suponha que $x \sim y$ . Devo provar que $\bar{x} = \bar{y}$ . Note que o queremos provar é uma igualdade de conjuntos, e pelo axioma da extensão da teoria de conjuntos, dois conjuntos são iguais se, e somente se, um está contido no outro.

Dito isto, o que devemos fazer é provar que $\bar{x} \subset \bar{y}$ e que $\bar{y} \subset \bar{x}$ .

Seja $z \in \bar{x}$ , daí decorre que $x \sim z$ pela definição de $\bar{x}$ . Pela simetria de $\sim$ podemos concluir que $z \sim x$ . Por hipótese temos que $x \sim y$ , portanto, é verdade que $z \sim x$ e $x \sim y$ . Então, pela transitividade de $\sim$ , temos que $z \sim y$ . Daí decorre que $y \sim z$ pela simetria de $\sim$ . Logo, $z \in \bar{y}$ pela definição de $\bar{y}$ , como queríamos demonstrar.

De forma análoga pode-se mostrar que $\bar{y} \subset \bar{x}$ . (Me desculpe por proferir essas palavras que irritam tanto quando lemos nos livros texto, mas juro que é análogo mesmo :’]). $\\ \hfill{\blacksquare}$

Agora que provamos este lema, estamos prontos para começar a última prova deste texto que é:

Proposição

Seja $A$ um conjunto não vazio e $\sim \,$ uma relação arbritária de $A$ . Então o conjunto quociente $A \setminus \sim$ é ele próprio uma partição.

Prova

Note que na definição de partição, as únicas propriedades que os elementos de um conjunto não vazio precisam possuir para o conjunto ser uma partição são:

Para todo $B_1$ , $B_2 \in \mathbb{P}$ , temos que $B_1 \neq B_2 \imp B_1 \cap B_2 = \emptyset$
$\bigcup\limits_{B_i \in \mathbb{P}} B_i = A$ , onde $i$ varia de $1$ até a cardinalidade de $\mathbb{P}$ .

Então devemos provar que os elementos de $A \setminus \sim$ satisfazem essas duas propriedades. Vamos lá:

Primeira propriedade:

Seja $\bar{x}, \bar{y} \in A \setminus \sim$ .

Suponha que $\bar{x} \neq \bar{y}$ . Devo provar que $\bar{x} \cap \bar{y}=\emptyset$ .

( $\subset$ ) Suponha por absurdo que $\exists a \in \bar{x} \cap \bar{y}$ , logo $a \in \bar{x}$ e $a \in \bar{y}$ , o que implica que $a \sim x$ e $a \sim y$ , e daí concluímos que $x \sim y$ . Mas, pelo lema que provamos, $x \sim y \imp \bar{x} = \bar{y}$ , o que contraria a nossa suposição de que $\bar{x} \neq \bar{y}$ .

( $\supset$ ) Há um teorema da teoria de conjuntos que diz que o $\emptyset$ está contido em qualquer conjunto, logo está contido em $\bar{x} \cap \bar{y}$ também.

Segunda propriedade:

Seja $\{\bar{x_i}\}$ a família dos conjuntos que são elementos de $A \setminus \sim$ . Vamos provar que:

$\bigcup\limits_{x_i \in A} \bar{x_i} = A$ .

( $\subset$ ) Pela definição de classe de equivalência junto com a definição de relação de equivalência, temos que $\bar{x} \subset A, \forall x \in A$ . Logo, $\bigcup\limits_{x_i \in A} \bar{x_i} \subset A$ .

( $\supset$ ) $x \in A \imp \exists \bar{x} \subset A$ tal que $x \in \bar{x}$ (pela propriedade reflexiva de uma relação de equivalência). Logo, $x \in \bigcup\limits_{x_i \in A} \bar{x_i}$ . $\\ \hfill{\blacksquare}$

Conclusão

O que fiz (ou pelo menos tentei) nesse post foi provar que se $\sim$ é uma relação de equivalência em $A$ então o conjunto das classes de equivalência $A \setminus \sim$ é uma partição de $A$ , e se $\mathbb{P}$ é uma partição de $A$ , então a relação $R$ induzida por $\mathbb{P}$ é uma relação de equivalência cujo conjunto das classes de equivalência $A \setminus R$ é exatamente $\mathbb{P}$ .

Isso significa que relações de equivalência particionam um conjunto, no sentido de que todo par de partes é disjunto, e a união da família das partes é o próprio conjunto.

Equivalentemente, podemos dizer que essas partes são uma maneira de agrupar os elementos do conjunto que está sendo particionado, de modo que cada elemento fica em exatamente uma parte.

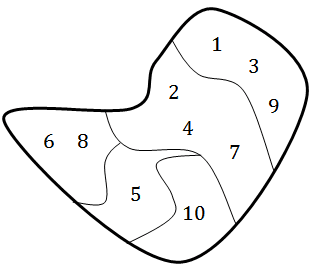
figura de um conjunto que foi particionado. Se criarmos o conjunto cujos elementos são essas partes, estaremos criando um conjunto quociente. — uma partição do conjunto dos números naturais menores que 11

Graças ao que foi feito nesse post, podemos tratar indiferentemente conjuntos quocientes e partições de um conjunto qualquer.

Intuitivamente, é fácil entender porque particionar um conjunto pode ser útil. Ao particionar um conjunto, podemos tratar suas partes como entes por si só e opera-las entre si.

E o melhor de tudo é que toda essa teoria nos dá um método para criar quantas partições você quiser em um conjunto: basta encontrar alguma relação de equivalência dentro desse conjunto. E isso é mais fácil do que parece.

Um exemplo de uma partição bastante estudada é o conjunto de vetores. Vetores são classes de equivalência de entes bem peculiares, chamados segmentos orientados.

Se quiser saber mais, leia o texto da minha colega de curso, onde ela se aprofunda nisso:

Diferença entre segmentos orientados e vetores (e mais!) – Iane Martins

Referências

Livro de onde tirei todas as provas e as definições: Introdução à Álgebra, do Adilson Gonçalves (esse cara foi orientador do meu professor de álgebra!!).

Prova de que um conjunto é quociente se e só se é uma partição

Prova de que toda partição é um conjunto quociente

Prova de que todo conjunto quociente é uma partição

Conclusão

Referências

Deixe um comentário Cancelar resposta