Resumo de Algoritmos Numéricos

Olá! Eu sou um estudante de matemática e acabei de fazer um curso (ou matéria) chamado Algoritmos Numéricos.

Esse curso é uma introdução à área da matemática chamada Algoritmos Numéricos, que estuda métodos numéricos para resolver problemas matemáticos.

Esse post é um resumo de todo o conteúdo que vi no curso.

Não haverá contas aqui. O objetivo do post é só organizar meus novos conhecimentos. Caso eu queira botar alguma conta que vi no curso aqui no blog eu faço um post a parte no futuro.

Introdução

A primeira aula do curso foi sobre o que são e por que usar métodos (ou algorítmos) numéricos.

Resumidamente, para mim os métodos numéricos são a arte de calcular boas aproximações de forma fácil.

Boas aproximações do que você se pergunta? Da solução de qualquer problema matemático!

Por exemplo: logo no começo do curso aprendemos um método (chamado regra dos retângulos a esquerda) para calcular uma aproximação de qualquer integral só fazendo contas de multiplicação e adição.

Então o motivo de usarmos métodos numéricos é que alguns problemas matemáticos podem ser difíceis (ou até impossíveis) de se resolver analiticamente (isto é, de forma exata) mas são fáceis de serem resolvidos numericamente.

Erros

Como os métodos numéricos nos dão soluções aproximadas, haverá um erro entre a solução obtida e a solução real, e por isso estudamos erros até o fim do curso, mas não falarei muito disso aqui no post.

Só falarei que há métodos numéricos mais precisos que outros e que o nome técnico do erro causado por métodos numéricos é erro de truncamento.

Obs: esse nome é horrível.

O que teve de Computação/Programação

A segunda aula do curso foi sobre como o computador armazena números.

Foi uma aula estranha porque ainda não tenho bagagem sobre computadores para entendê-la, mas uma coisa importante que aprendi nela é: o computador só consegue armazenar uma malha finita da reta real, e ele tem que arredondar todos os números que estão fora dessa malha por números que estão dentro dela.

Isso é inclusive uma das causas de um outro tipo de erro, que pode estar presente tanto nos métodos numéricos quanto nos analíticos: o erro de arredondamento.

A segunda aula foi a única aula exclusiva sobre computação, mas para não perder o embalo registrarei aqui tudo que aprendi de interessante sobre programação durante o curso:

• O python é uma linguagem de programação.
• Linhas com igualdade criam caixinhas. O lado esquerdo da igualdade é o nome da caixinha e o lado direito da igualdade é o que ta dentro da caixinha (até aquela linha).
• É muito importante entender a ordem em que o computador lê as linhas de código, que é de cima pra baixo.
• Acho que o valor armazenado numa variável depois de um loop é o último valor registrado no loop.
• O loop também é lido de cima pra baixo, mas quando acaba a última linha ele volta para a primeira linha do loop. Isso continua valendo para loops dentro de loops. Nesse caso, ele só volta para o loop de fora quando acaba o loop de dentro, e quando o loop de fora chegar no loop de dentro ele começa o loop de dentro de novo.
• Quando você coloca um ‘input’ num código você passa a poder executar ele como .py, que é muito mais leve do que abrir uma IDE. Maas, é bom colocar uma linha escrito: ‘input(“Pressione Enter para fechar…”)’ para ele não fechar o .py antes de printar o que você quer ver.
• Uma forma inteligente de entender o que o loop ta fazendo é testá-lo mentalmente para os casos limites.
• Códigos que executam tarefas “simples” podem facilmente passar de 400 linhas. Isso é um absurdo pra mim.
• Programar interfaces com o usuário é de longe a parte mais difícil de um código, acho que isso é o que separa um bom programador de um ruim.

(teoricamente o curso assume que você saiba programação. Mas mesmo sem saber programar eu consegui passar porque só havia 1 questão de programar em cada prova)

O que teve de Matemática

Finalmente chegamos na parte matemática do curso. Ela começou na terceira aula e se estendeu até a última aula.

Nessa parte, aprendemos a resolver via métodos numéricos uma ampla variedade de problemas matemáticos. Falarei um pouco sobre todos eles abaixo.

Esses métodos foram pensados bem antes da existência de computadores, então obviamente não é necessário saber programar para entende-los. Mas até que alguns são fáceis de serem programados, o difícil mesmo é programar uma interface com o usuário para utiliza-los como programas.

Falarei dos métodos na ordem em que vimos, separando-os por primeira prova (P1) e segunda prova (P2).

Primeira prova

Resolução de sistemas n x n

O primeiro problema matemático que aprendemos a resolver numéricamente foi o de resolver sistemas lineares de tamanho n x n que tenham única solução.

Aprendemos 3 algoritmos para isso, o Eliminação de Gauss, o Gauss-Jacobi e o Gauss-Seigel.

O Eliminação de Gauss é o famoso escalonamento que aprendemos em Álgebra Linear 1. É chato de fazer as contas mas resolve.

Eu já não lembro mais nada do Gauss-Jacobi e o Gauss-Seigel, mas acho que eles são parecidos com o Eliminação de Gauss.

Ajuste de curvas

O segundo problema que atacamos foi o de ajustar curvas 2D em um conjunto de pontos dados do plano. O objetivo é que a curva ajustada esteja o mais perto possível de todos os pontos.

(acho que também aprendemos a ajustar superfícies 3D em um conjunto de pontos do espaço, mas não lembro)

Para resolver esse problema, foi ensinado os métodos Regressão linear simples e Regressão linear múltipla.

Confesso que esses foram os únicos algoritmos em que eu não entendi absolutamente nada das suas deduções. Elas envolvem inventar um erro e resolver um sistema de EDPs, assunto que eu nunca nem cheguei a estudar.

Se algum dia eu conseguir programar esse código sem consultar nada direi que sei bastante matemática e programação.

Apesar da dificuldade, esse com certeza é um dos problemas mais importantes que nós resolvemos. Consigo imaginá-lo tendo utilidades para um estatístico que quer analisar dados que estão relacionados.

Para usarmos o algorítmo de ajustar curvas a um conjunto de pontos, primeiro você escreve a curva que quer ajustar nessa forma:

onde as podem ser qualquer função que você quiser.

Daí os são encontrados resolvendo o seguinte sistema linear:

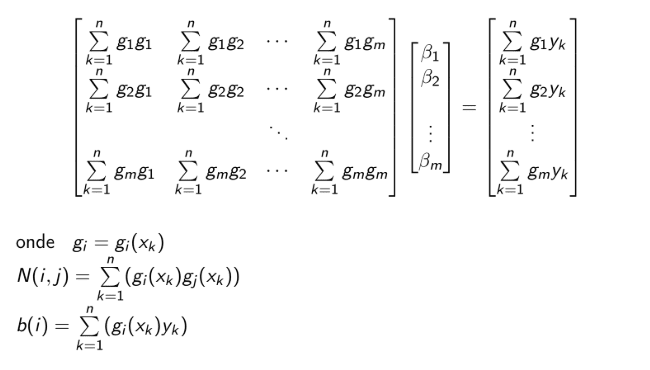
com sendo os k pontos a serem ajustados.

Você pode resolver esse sistema escalonando.

Cálculo de raízes de funções de 1 variável

O terceiro problema que atacamos foi o de encontrar raízes de funções contínuas de 1 variável.

Para esse, nos foi ensinado três métodos numéricos: o Método da bisseção, o Método de Newton/Raphson e o Método da tangente.

A ideia do método da bisseção é encontrar um intervalo em que a função muda de sinal. Como a função é contínua, então necessáriamente tem que haver pelo menos uma raiz nesse intervalo. Daí você divide o intervalo pela metade e verifica em qual parte a função continua trocando de sinal. Faça isso iteradamente e pare quando o intervalo tiver pequeno o suficiente para ser uma boa aproximação da raiz.

Já o método de Newton/Raphson consiste em escolher um ponto da função e calcular a equação da reta tangente a função nesse ponto. Depois você calcula a interseção dessa reta tangente com o eixo x. Essa interseção será a aproximação da sua raiz. Caso queira melhora-lá, é só repetir o processo.

O método de Newton/Raphson era o único método numérico que eu já conhecia, pois li no livro o Romance das Equações Algébricas, há 5 anos atrás.

Um gif que elucida bem como o método de Newton/Raphson funciona é:

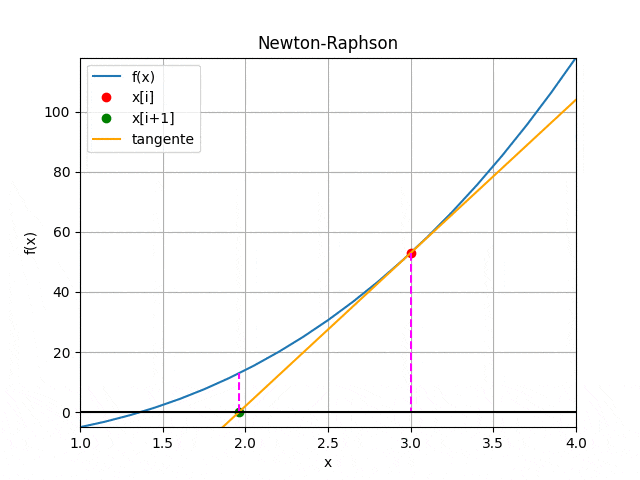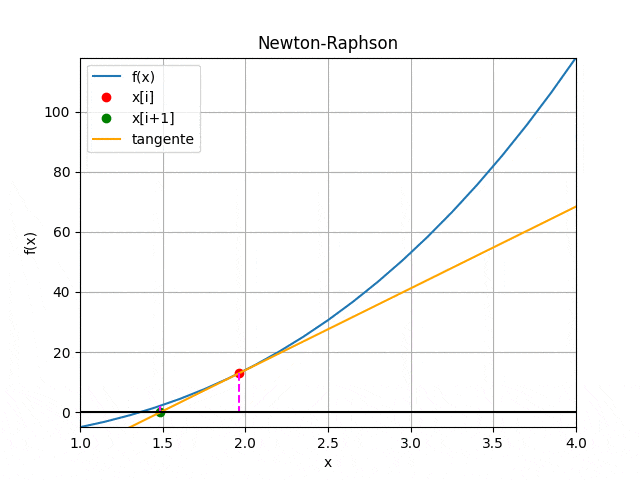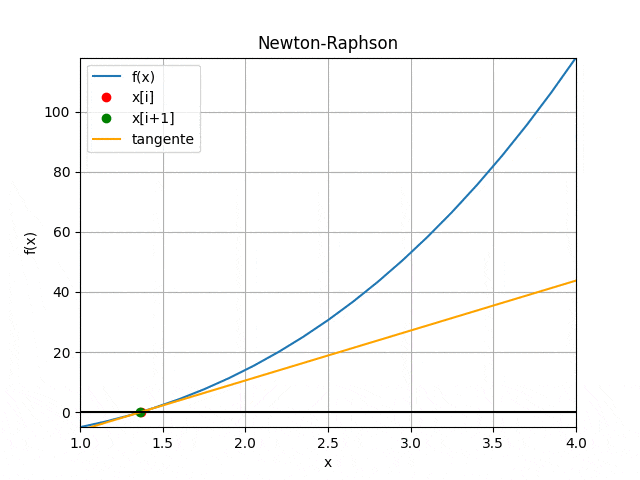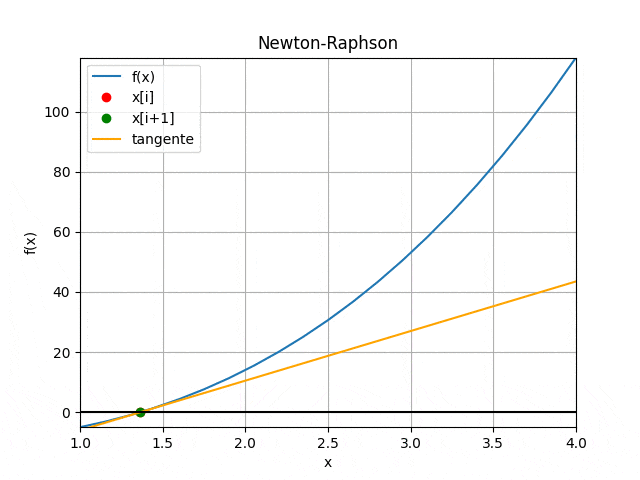
(note que dependendo do gráfico da função o método de Newton/Raphson não converge para a raiz)

Também foi ensinado o método da Tangente, que é uma variação do método de Newton/Raphson e que possui menor custo computacional, eu acho (não lembro como é esse).

A fórmula do método de Newton/Raphson é:

onde é o ponto inicial escolhido e todas as abscissas dos pontos a partir de são aproximações da raiz procurada.

(essa fórmula eu consegui deduzir sem olhar em nada para escrever no post :D)

Foto da primeira prova

Segunda prova

Resolução “pontual” de uma EDO de primeira ordem

O quarto problema que aprendemos a resolver numericamente foi o de encontrar os pontos que quiser da solução de uma EDO de primeira ordem que possui uma condição inicial.

Para esse problema vimos 3 métodos numéricos (que se ramificam em novos métodos): o método de Euler, os métodos baseados na série de Taylor e os métodos de Runge-Kutta.

A ideia do método de Euler é calcular sucessivas aproximações lineares. Isto é, primeiro você calcula a reta tangente ao ponto dado pela condição inicial da EDO e depois você calcula uma aproximação de algum ponto próximo calculando a imagem de sua abscissa na reta tangente calculada.

Por incrível que pareça eu já falei de algo bem próximo do método de Euler aqui no blog (mas sem saber que era isso), no post:

Como calcular uma raiz quadrada não exata – Quarto 707

Eu provavelmente vou esquecer 90% do que vi nesse curso, mas acho que o método de Euler eu vou guardar.

Além do método de Euler, também vimos o método da série de Taylor de 2 ordem o método de Runge Kutta.

O método da série de Taylor de 2 ordem é o mesmo que o método de Euler, mas nesse calculamos a “parábola tangente” ao ponto dado pela condição inicial e depois calculamos a imagem do ponto que se quer conhecer na parábola. Dessa forma estamos levando em consideração a curvatura da função também.

Um erro da minha intuição era achar que os pontos precisavam ser as extremidades da parábola, mas isso não é verdade. O que fazemos na verdade é ligar os pontos por arcos de parábolas. Sabendo disso fica mais fácil de imaginar o que está acontecendo de fato.

Por exemplo, suponha que você queira calcular quanto vale a solução da seguinte EDO em :

Pelo método da série de Taylor de 2 ordem, a párabola tangente ao ponto tem equação .

Logo, o valor da párabola em é . Essa é a nossa aproximação, enquanto o valor real é aproximadamente .

Geometricamente, o que fizemos foi:

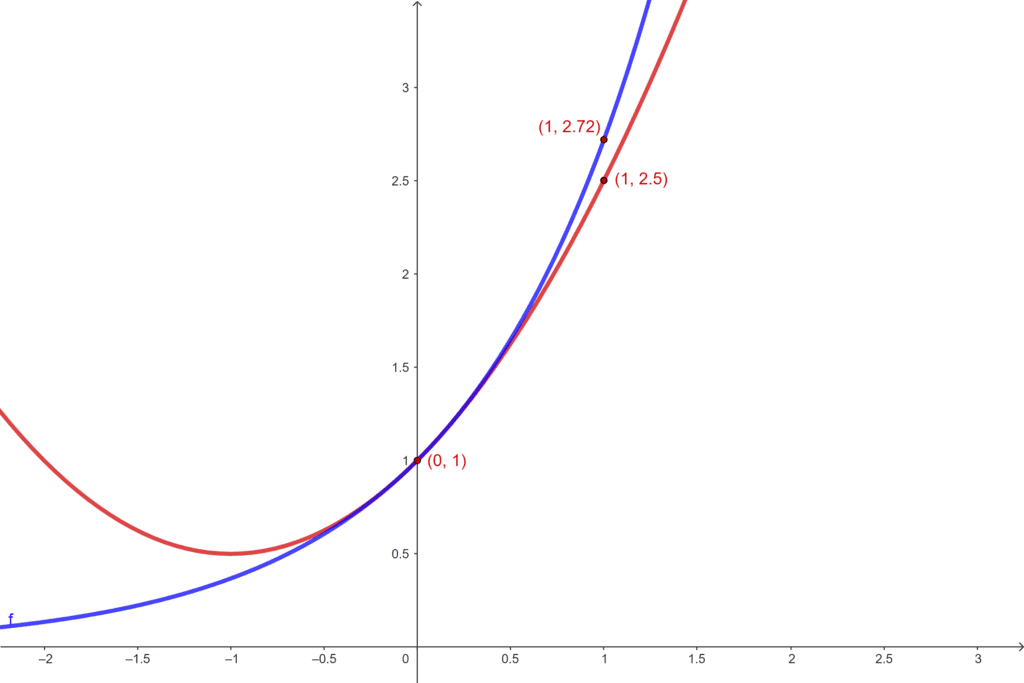
Mas, na minha cabeça, o que estávamos fazendo era algo tipo isso:

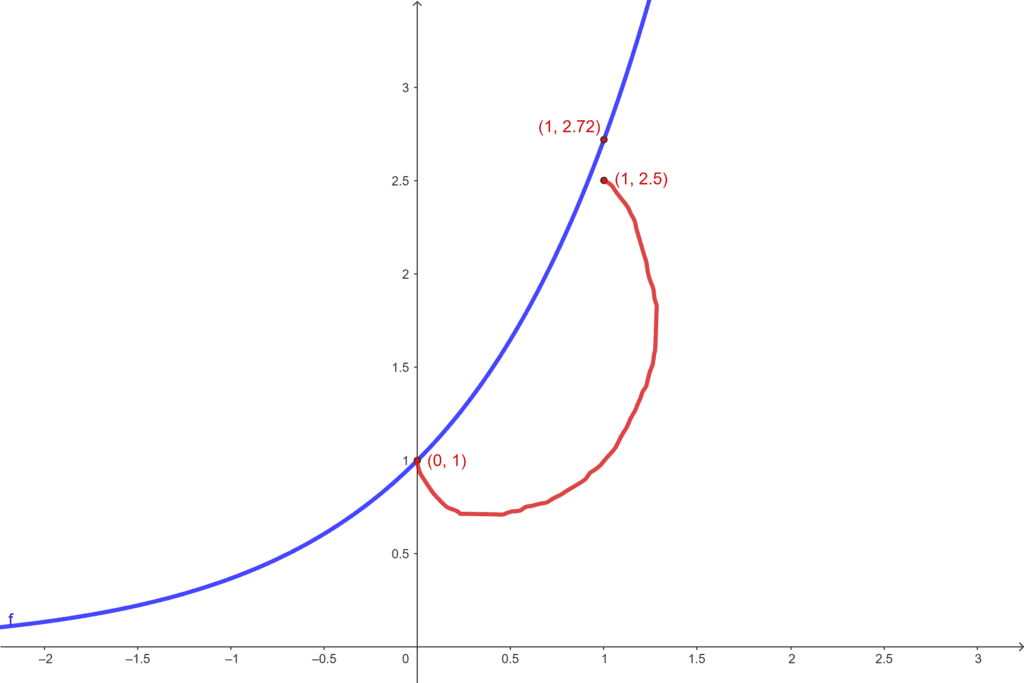
Sei que não faz sentido mas foi o que imaginei quando minha professora estava explicando esse assunto.

Um problema dos método da série de Taylor é que neles precisamos fazer uma derivada parcial (com direito a regra da cadeia pra duas variáveis num caso bem particular).

Ou seja, tanto no métodos da série de Taylor quanto no algorítmo de ajustar curvas a gente lida com derivadas parciais, assunto que eu não domino nenhum um pouco.

Já o método de Runge Kutta calcula dois coeficientes angulares diferentes para melhorar ainda mais a aproximação da solução. Esse eu tive que dar a vida pra entender por causa de uma confusão, e sei que esquecerei em breve.

A fórmula do método de Euler é:

onde é o ponto conhecido pela condição inicial da EDO, é o ponto procurado e é .

Resolução “pontual” de um sistema de EDOs de primeira ordem

O quinto problema foi o de encontrar pontos pertencentes a soluções de um sistema de EDOs de 1ª ordem, quando se tem condições iniciais.

O algorítmo é praticamente o mesmo do de cima, com a exceção de que nesse calculamos os pontos das soluções simultaneamente.

Incrível como um problema que eu nem sei resolver analiticamente fica fácil de se resolver numéricamente. Pena que dá muita conta, por isso precisamos de computadores para executar os métodos numéricos.

Resolução “pontual” de uma EDO de ordem n

O sexto problema foi o de encontrar pontos de soluções de EDOs de ordem n, quando se tem condições iniciais.

Para resolver EDOs de ordem n, você faz uma substituição de variáveis e cai num sistema de EDOs de primeira ordem de n equações.

A mudança de variáveis é estranha, e parece mágica isso dar certo, mas dá.

Interpolação de um conjunto de pontos dado por polinômios

O sétimo problema é o de interpolar pontos dados por um polinômio.

Esse problema pode parecer o mesmo que o de ajustar curvas, mas não é. A diferença entre interpolar funções e ajustar curvas é que na interpolação a função é obrigada a passar por todos os pontos, e no ajuste de curvas não.

Nos foram ensinados dois métodos numéricos para interpolar pontos por polinômios: o método por sistema e o forma de Newton (mas já vi um outro método, chamado de método de Lagrange, quando fiz Matemática Básica II)

Em ambos os métodos, você interpola 2 pontos por um polinômio de grau 1, 3 pontos por um polinômio de grau 2 e assim vai…

Caso você queira interpolar n pontos por um polinômio de grau maior que n-1, haverão infinitos polinômios diferentes como opção. Ou seja, por 3 pontos passam infinitas cúbicas, quárticas e etc.

No método por sistema, tudo o que você faz é substituir os pontos na equação do polinômio que você vai usar para interpolar. Se forem n pontos, você cai num sistema de n equações. Daí você resolve o sistema escalonando.

Já o forma de Newton é um jeito de interpolar polinômios fazendo umas diferenças malucas lá.

O forma de Newton da muuito trabalho. Sempre que você for interpolar um polinômio usando ele você precisa fazer uma tabela. Eu cheguei a chamar o Newton de burro por causa disso, mas seu método é o que tem menor custo computacional. Ou seja, eu que sou o burro aqui.

É interessante notar que os polinômios obtidos pelos dois métodos são iguais. Mas cada método escreve ele de uma forma diferente.

Como no problema passado aprendemos algoritmos que nos dão pontos de uma solução de uma EDO, se você juntar algum dos algoritmos passados com um desses para interpolar polinômios você obtém um algorítmo completo para resolver EDOs numericamente.

O problema é que caso você queira interpolar muitos pontos (tipo uns 20), esses dois métodos são horríveis. A professora falou que, nesse caso, o melhor a se fazer é interpolar por partes, 4 pontos de cada vez, por um polinômio de grau 3. Daí também é interessante exigir que os pontos de fronteira tenham a mesma curvatura, para que o polinômio seja suave. Mas fazer isso só com papel e caneta é inviável de todo jeito.

Para interpolar o polinômio de grau n

nos n+1 pontos , , … , , basta resolver o seguinte sistema linear:

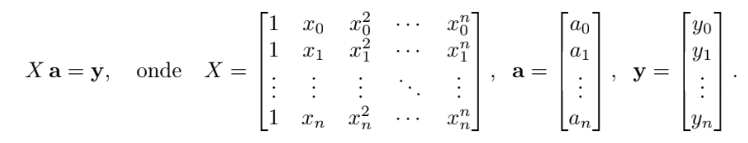
para obter os coeficientes do polinômio.

A matriz é conhecida como matriz de Vandermonde.

Uma possível maneira de resolver esse sistema linear é escalonando.

Integração de integrais definidas

O oitavo e último problema que atacamos numéricamente foi o de calcular uma integral definida.

O primeiro método numérico ensinado para isso foi o retângulos a esquerda (ou direita).

Esse algorítmo é extremamente simples e fornece aproximações decentes para qualquer integral que você se deparar.

O algoritmo consiste em aproximar a área abaixo da função por retângulos. É o mesmo que a soma de Riemann, mas sem fazer a quantidade de retângulos tender ao infinito.

O outro algorítmo é o Newton-Cotes.

A ideia desse é aproximar a função por um polinômio e integra-lo, já que integrar polinômios é fácil. Por isso, ele deve ser usado em conjunto com o algorítmo anterior de interpolar pontos.

A integração da bastante conta, mas só precisamos faze-la uma vez para obter uma fórmula.

Se o polinômio tiver grau 1 você obtém a regra do trapézio.

Se você integrar um polinômio de grau 2 você chega na regra de 1/3 de Simpson.

Se você integrar um polinômio de grau 3 você chega em uma outra fórmula, e assim vai.

Muito cuidado, pois para interpolar uma parábola você precisa de 3 pontos, então a regra 1/3 de Simpson vai levar isso em consideração.

O último método para integrar funções se chama quadratura Gauss-Legendre e eu não entendi praticamente nada dele. Só entendi que, aparentemente, mudar variável é a coisa mais útil da matemática.

A fórmula para a regra do retângulos a esquerda é:

   

onde , , e .

Foto da segunda prova

Diario de estudos

Como usarei esses conhecimentos

O que mais gostei do curso não foi a parte de programação, mas sim a parte de matemática. É muito interessante que os algoritmos que vimos possam ser usados só com papel e caneta, mesmo alguns dando uma boa quantidade de contas.

Esses algoritmos são uma excelente alternativa para resolver problemas de matemática de forma aproximada quando eu não souber resolver analiticamente, como por exemplo sistemas de EDOs (eu não sei resolver sistemas de EDO analiticamente, mas sei numericamente vei!)

Acho que os algoritmos que usarei no meu dia a dia são o retângulos a esquerda, que usarei sempre que me deparar com uma integral definida e estiver com preguiça de pensar em como resolve-la, e o método de Euler, que provavelmente terá utilidade quando eu for tentar resolver alguma EDO que aparece quando estudamos física.

O que preciso para entender um computador

O começo desse post pode ser visto como uma continuação do meu outro post:

Dúvidas de lógica para o meu eu do futuro parte 2

Se eu juntar o que vi sobre como o computador armazena números, com a lógica feita a partir de Alan Turing, o NandGame e Eletromagnetismo, serei capaz de entender como funciona um computador.

O bom é que a lógica a partir de Turing, assim como a lógica anterior dele, ainda é feita com teoria de conjuntos, então teoricamente esse conhecimento deve ser acessível pra mim se eu estudar muito, diferentemente de Eletromagnetismo, que ainda parece coisa de outro mundo pra mim ;-;.

Acho que foi Turing quem definiu computabilidade e, consequentemente, número computável.

Esse é o último curso de caráter computacional da graduação, então eu provavelmente nunca mais programarei na minha vida.

O que faz um engenheiro

Eu fiz esse curso junto com uma turma de Engenharia Elétrica. Como esse curso foi pensado muito mais para eles do que para os matemáticos, aproveitei a experiência para pensar no que um engenheiro faz em seu trabalho.

Acho que os engenheiros precisam aprender métodos numéricos para resolver problemas matemáticos porque as contas da vida real são horríveis, e são elas que aparecem quando tentamos construir algo na vida real usando a matemática.

Daí, um bom engenheiro deve saber bons métodos numéricos para fazer as contas do seu trabalho, programação para programar os métodos numéricos (ou pelo menos entender como funciona os programas que ele vai usar) e saber trabalhar com erros.

Além disso, eles precisam saber modelar o mundo, para poder usar tudo isso.

Resumindo, um engenheiro precisa saber as partes da matemática e da programação que o permita construir tecnologias.

Coisas legais que relembrei

O problema de interpolar funções me fez lembrar do polinômio de Lagrange, que eu vi em 2022 quando entrei na faculdade! Aí eu fui ver se ainda conseguia usa-lo sem consultar nada e consegui interpolar 3 pontos quaisquer que eu escolhi, hehe.

Outra coisa que eu já sabia era o método de Newton. Li sobre ele antes mesmo de estudar cálculo, lá em 2020, no livro ‘O Romance das Equações Algébricas’. Não sei se aprendi quando li nessa época, mas há muito tempo eu já me sinto confortável usando esse método.

Uma coisa legal que essa matéria me fez exercitar é desenhar gráficos de funções que eu não decorei o gráfico. A forma mais eficiente de fazer isso é decorando alguns gráficos e elementares e saber o que cada operação numa função faz no seu gráfico, conteúdo que vi no Noções de Matemática volume 1 (ainda em 2020) e em Matemática Básica 1 (em 2022), e que venho usando desde então. Apesar de ser básico e eu saber fazer, eu definitivamente ainda não automatizei isso na minha cabeça.

Rever EDOs depois de ter feito Cálculo 4 no semestre passado foi uma experiência interessante. Durante uma das aulas de Algoritmos me caiu a ficha de que para resolver algumas EDOs, basta literalmente só integrar um lado da equação em relação a y e o outro lado da equação em relação a x. Uma EDO que pode ser resolvida assim é: . É tão bobo, mas eu não tenho ideia do porque isso dá certo. Acho que essa é a forma normal de como resolvemos EDOs separáveis.

Coisas legais que aprendi

Fazendo exercícios desse curso eu percebi que não tem nenhuma integral que eu tenha algum interesse genuino nela. Todas as integrais são iguais para mim, pois não há nenhuma região específica que eu tenha curiosidade de calcular a área ou volume. Talvez no máximo seja interessante modelar meu volume como a integral de uma função de duas variáveis e calcula-la no futuro. Acho que isso mudaria se eu pensasse em integrais como somas infinitas de infinitesimais não só de áreas ou volumes, mas de ideias. Sob essa interpretação deve ser mais fácil encontrar alguma integral que eu tenha interesse em resolver. Me pergunto como seriam essas contas.

Uma coisa super interessante que aprendi nesse curso é a interpretação geométrica de um escalonamento de um sistema 2×2. O que fazemos no escalonamento é alterar uma das retas dos sistema por uma reta horizontal que também passa pela solução do sistema.

Outra coisa legal que aprendi é que pra saber quantas operações um algoritmo faz é literalmente só fazer ele para um caso geral e contar as operações. Apesar de der fácil explicar, eu nunca fiz isso pra saber se é só isso mesmo.

Outra coisa legal que aprendi é que o grau de um polinômio mede quantas “parábolas” ele tem. Um polinômio de grau n tem n-1 “parabolas”. É por isso que o seno é um polinômio infinito, porque ele tem infinitas “parábolas”. Acho que fica melhor se eu trocar a palavra parábola por volta, mas sei la.

Uma dúvida que sempre tive é por que temos que saber Álgebra Linear para programar. Fazendo esse curso eu concluí que é porque muitos problemas matemáticos podem ser resolvidos modelando-os com os sistemas lineares certos.

Por fim, queria dizer que ao usar o método da série de Taylor de 2ª ordem para resolver uma EDO trigonométrica, eu caí numa curva que não era um polinômio. Então o nome “parábola tangente” que usei no post é horrível, pois ela nem sempre será uma parábola. Além disso, mesmo que ela seja uma parábola, ela pode cortar o gráfico da função, como ocorreu aqui.

Muito obrigado por chegar até aqui :]