Dedução da soma dos quadrados dos n primeiros naturais

Neste post deduzirei quanto é a soma dos quadrados dos $n$ primeiros números naturais. Isto é, encontrarei uma fórmula para calcular o valor de

$1^2 + 2^2 + 3^2 + … + n^2$

para qualquer $n$ que você queira escolher.

A dedução que apresento aqui é bem pessoal, pois não a vi em lugar nenhum e usei conhecimentos que eu já havia internalizado mas que não necessariamente são conhecidos por todo estudante.

Resumindo, apresentarei a forma com que consegui atacar o problema, e que, graças a Deus, deu certo (só precisei de 2 semanas pra conseguir xD).

---

— publicidade —

Dedução

Seja $x$ a soma dos quadrados dos $n$ primeiros naturais. Isto é:

$x = 1^2+2^2+3^2+\dots+n^2$

O que queremos é encontrar uma expressão bonita para $x$.

A minha ideia central foi enxergar cada parcela de $x$ como uma outra soma, pois eu sei que todo quadrado perfeito é a soma dos primeiros números ímpares. Isto é, eu enxerguei $x$ da seguinte forma:

$x = (1)+(1+3)+(1+3+5)+(1+3+5+7)+\dots+(1+3+5+7+…+2n-1)$

A vantagem de enxergar assim é que nos livramos das potências, e agora as únicas operações da expressão são somas. Logo, podemos escrevê-la como um somatório mais simples.

Para isso, precisamos observar que :

• o $1$ aparece $n$ vezes;
• o $3$ aparece $n-1$ vezes;
• o $5$ aparece $n-2$ vezes;
• e assim por diante, até o $2n-1$, que aparece $1$ vez.

Logo, temos que

$x= n\cdot1+(n-1)\cdot3+(n-2)\cdot5+\dots+1\cdot(2n-1)$.

E em notação de somatório isso fica:

$$ x = \sum_{k = 1}^n ((n+1-k)(2k-1)) $$

(enxergar esse somatório só não foi mais difícil que pensar em transformar todos os quadrados em somas de ímpares)

E agora o problema praticamente acabou, basta fazer contas partindo desse somatório usando as propriedades dos somatórios. Recomendo que tente sozinho antes de prosseguir. As contas são:

$ \begin{aligned} x & = \sum_{k = 1}^n ((n+1-k)(2k-1)) \\ & = \sum_{k = 1}^n (2kn-n+2k-1-2k^2+k) \\ & = \sum_{k = 1}^n 2kn+\sum_{k = 1}^n-n + \sum_{k = 1}^n 2k+\sum_{k = 1}^n -1+\sum_{k = 1}^n -2k^2 + \sum_{k = 1}^n k \\ & = 2n \sum_{k = 1}^n k-n \sum_{k = 1}^n 1+2 \sum_{k = 1}^n k-\sum_{k = 1}^n 1-2 \sum_{k = 1}^n k^2+\sum_{k = 1}^n k \end{aligned} $

Notando que:

• $\sum_{k = 1}^n k = \frac{n(n+1)}{2}$, pois isso é uma PA cujo primeiro termo é $1$ e o último é $n$;
• que $\sum_{k = 1}^n 1 = n$, pois isso é o mesmo que somar $1$ $n$ vezes;
• e que $\sum_{k = 1}^n k^2 = x$, pois é exatamente isso que queremos calcular, teremos que:

$ \begin{aligned} x & = 2n \sum_{k = 1}^n k-n \sum_{k = 1}^n 1+2 \sum_{k = 1}^n k-\sum_{k = 1}^n 1-2 \sum_{k = 1}^n k^2+\sum_{k = 1}^n k \\ & = 2n\frac{n(n+1)}{2}-n\cdot n+2 \frac{n(n+1)}{2}-n-2x+\frac{n(n+1)}{2} \\ & = (n^2+n)n-n^2+n^2+n-n-2x+\frac{n^2+n}{2} \\ & = n^3+n^2-2x+\frac{n^2 + n}{2} \end{aligned} $

Passando o $2x$ para o lado esquerdo da igualdade obtemos que:

$$3x = \frac{2n^3+2n^2+n^2+n}{2}$$

E, portanto:

$$ x = \frac{2n^3+3n^2+n}{6} $$

E esta é a formula para a soma dos quadrados dos $n$ primeiros números naturais!

Confesso que me surpreendi bastante quando cheguei na fórmula correta. E fiquei bem feliz também.

Usando a fórmula

Agora que deduzimos uma fórmula para a soma dos quadrados dos $n$ primeiros números naturais, somos livres para usá-la.

Se escolhermos $n = 7$ então:

$$ 1^2+2^2+3^2+4^2+5^2+6^2+7^2 = \frac{2\cdot7^3+3\cdot7^2 +7}{6} = 140 $$

Caso não tivesse os quadrados, o resultado seria:

$$ 1+2+3+4+5+6+7 = 28 $$

Bem interessante ver a diferença entre os dois resultados.

Diário de estudos

Atualmente estou fazendo a matéria Matemática Discreta na faculdade, e um dos primeiros problemas que o professor passou foi justamente esse do post. Como eu disse no início, eu fiquei duas semanas tentando resolver ele depois do professor o ter sugerido, e tive que resistir à tentação de olhar a solução todo esse tempo. Resolver esse problema foi uma vitória completa.

A ideia de escrever cada parcela como uma soma só me ocorreu pois, no começo desse ano, li um livro chamado ‘O poder do infinito‘, que me falou que todo quadrado perfeito é a soma de ímpares e que Galileu usou isso pra estudar os corpos em queda livre. De fato, somos o que fazemos todos os dias.

Depois de eu conseguir resolver esse problema meu professor o corrigiu, mas minha solução foi diferente da solução dele. Caso tenha interesse em ver como ele fez, veja:

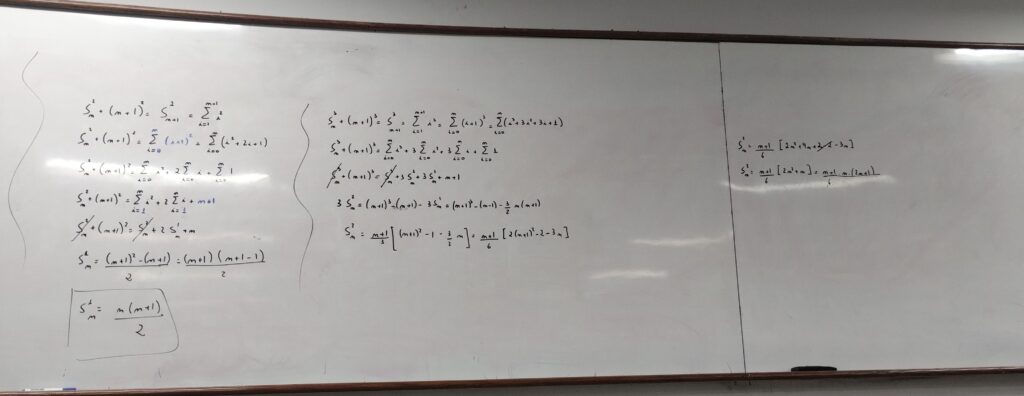
O interessante da solução do professor é que ela pode ser adaptada para deduzirmos fórmulas para a soma dos cubos, das quartas potências e assim por diante.

Caso tenha gostado desse post, leia também:

Dedução da soma dos termos de PG’s finitas e infinitas – Quarto 707

Muito obrigado por chegar até aqui ^^

---

— publicidade —