Nesse post deduzirei quantos grafos simples com $n$ vértices rotulados existem e outras coisas mais.
Sempre que eu escrever ‘grafo’ daqui em diante, estarei me referindo a um grafo simples.
— publicidade —
Conteúdo do post
Seja $V$ um conjunto de vértices que tenha $n$ elementos.
Todo grafo é determinado por um conjunto de vértices e um conjunto de arestas. Por isso, para determinarmos quantos grafos cujo conjunto de vértices é $V$ existem, basta saber quantos conjuntos de arestas conseguimos formar com os elementos de $V$, pois para cada conjunto de arestas teremos um grafo diferente.
Número máximo de arestas
Para começar será útil calcular o número máximo de arestas que podemos formar usando os vértices de $V$.
Para formar uma aresta precisamos escolher seus dois vértices. Pelo PFC, o número total de possibilidades que temos de fazer isso é $n \cdot (n-1)$, pois temos $n$ escolhas possíveis para o primeiro vértice e, para cada uma delas, $n−1$ escolhas possíveis para o segundo, já que não podemos escolher o mesmo vértice duas vezes. Assim, obtemos $n(n−1)$ pares ordenados de vértices. No entanto, como uma aresta é determinada por um par não ordenado de vértices, cada aresta foi contada exatamente duas vezes: uma vez como $(v_1, v_2)$ e outra como $(v_2, v_1)$. Portanto, devemos dividir esse total por $2$. Logo, o número de arestas possíveis é
\[ \frac{n \cdot (n-1)}{2} \]
Outra forma de calcular o número máximo é notar que o queremos é todas as possibilidades de escolher $2$ elementos dentre $n$ elementos. E isto é a seguinte combinação: ${n \choose 2} = \frac{n \cdot (n-1)}{2}$.
Quantos grafos existem
Seja $A$ o conjunto de todas as arestas formadas pelos elementos de $V$.
Como calculamos o número máximo de arestas, sabemos que $A$ tem exatamente $\frac{n \cdot (n-1)}{2}$ elementos.
E note que cada subconjunto de $A$ é um conjunto de arestas diferente, e portanto, define um grafo (já que fixamos os vértices). Então nosso problema se resume a saber quantos subconjuntos $A$ tem.
Para formar um subconjunto de $A$, precisamos escolher se cada aresta vai pertencer ao subconjunto ou não. Isto é: para a primeira aresta, podemos escolhê-la ou não. Para a segunda, podemos escolhê-la ou não. Para a terceira a mesma coisa, e assim vai até fazermos $\frac{n \cdot (n-1)}{2}$ escolhas. Logo, pelo PFC, há
\[ 2 \cdot 2 \cdot 2 \cdot … \cdot 2 = 2^{\frac{n \cdot (n-1)}{2}} = 2^{{n \choose 2}} \]
conjuntos de arestas.
Como nosso conjunto de vértices está fixado, cada conjunto de arestas vai determinar um grafo, e portanto esse também é o número de grafos rotulados com $n$ vértices existentes.
E se fixarmos o número de arestas?
O problema do título já foi resolvido, mas e se quisermos, além de fixar o número de vértices, também fixar o número de arestas?
Em outras palavras, quantos grafos com $n$ vértices e $m$ arestas existem?
Obviamente, o número de arestas fixado $m$ tem que ser menor ou igual a ${n \choose 2}$.
Para resolver esse problema, note que o que queremos é quantos subconjuntos de $m$ elementos o $A$ tem. E, como $A$ tem ${n \choose 2}$ elementos, isso é exatamente
\[ {{n \choose 2} \choose m} \]
Aplicando os resultados no caso n = 4
Até aqui deduzimos duas fórmulas úteis para estudar os grafos simples. Vamos agora somente usar essas fórmulas e ver o que obtemos.
Vejamos quantos grafos com 4 vértices existem e depois quantos grafos com 4 vértices e 6 arestas existem.
Seja $V = \{a, b, c, d \}$ nosso conjunto de vértices.
O número máximo de arestas que um grafo com 4 vértices pode ter é ${4 \choose 2} = 6$. Logo, o nosso $A$ nesse caso tem 6 elementos. De fato, $E = \{ \{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\}, \{c, d\} \}$.
Então, o número de grafos com $4$ vértices existentes é $2^{4\choose 2} = 2^6 = 64$.
Pode parecer muito, mas fica mais claro quando percebemos o quanto os vértices importam. Por exemplo, os grafos:
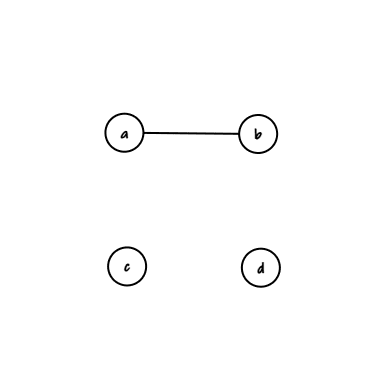
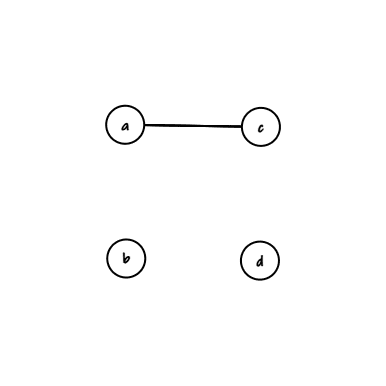
se parecem muito, mas são grafos diferentes.
Continuando… o número total de grafos com 4 vértices e 6 arestas é ${{4 \choose 2} \choose 6} = {6 \choose 6} = 1$
E, de fato, só há $1$ grafo com $4$ vértices e $6$ arestas, que é o grafo completo:
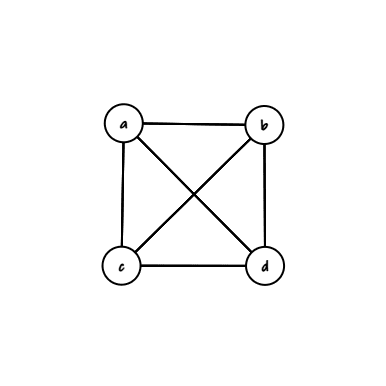
Obs: note que se quantos grafos com número de arestas maior que $6$, como $7$ por exemplo, existem, cairíamos na combinação ${6 \choose 7}$, que não faz sentido.
Comentários sobre o que fizemos
Nesse post eu determinei quantos grafos com $n$ vértices existem. No entanto, muitos deles são isomorfos entre si, como esses 2 -link-, por exemplo. Para calcular quantos grafos com $n$ vértices existem a menos de isomorfismo (isto é, quantos grafos com $n$ vértices não rotulados existem) é muito mais difícil e eu nem sei fazer isso.
Uma continuação mais suave do que fizemos nesse post poderia ser: “quantos grafos existem se fixarmos os graus dos $n$ vértices? “. Esse problema é mais difícil, pois nele também temos que olhar para a estrutura dos graus fixados. Uma observação importante é que o número total de vértices com grau ímpar tem que ser par, pois isso é um teorema da Teoria dos Grafos simples. Além disso, a soma dos graus tem que ser um número par, pois é igual a duas vezes o número de arestas do grafo.
Diário de estudos
Atualmente estou fazendo Matemática Discreta, e grafos é o conteúdo da terceira prova dessa matéria. Foi estudando para ela que descobri tudo isto que está no post. Eita matéria difícil!
Os exercícios que me nortearam a fazer essas descobertas foram:

Pra finalizar, eu queria dizer que mesmo antes de começar o curso eu já estava maturando a ideia de fazer um “grafo da Matemática”, isto é, um grafo onde cada vértice é um axioma/teorema e dois vértices são adjacentes se um é usado diretamente na prova do outro.
Meu plano inicial era fazer um hipergrafo orientado pois usamos conjuntos de hipóteses na prova de um teorema, mas mesmo fazendo isso no python, era horrível de ler o hipergrafo. Por isso, recentemente optei por fazer apenas um grafo orientado. Isso fará meu projeto perder um pouco de rigor, pois se perde a informação de qual é o conjunto suficiente de hipóteses para provar o teorema.
Além disso, esse ‘diretamente usado’ é muito vago, mas não tive escolha a não ser definir assim pois não sei como fazer de outra forma. Pelo menos isso destacará minhas peculiaridades, já que será o que é “diretamente” na minha opinião.
Por enquanto meu grafo da matemática está assim:
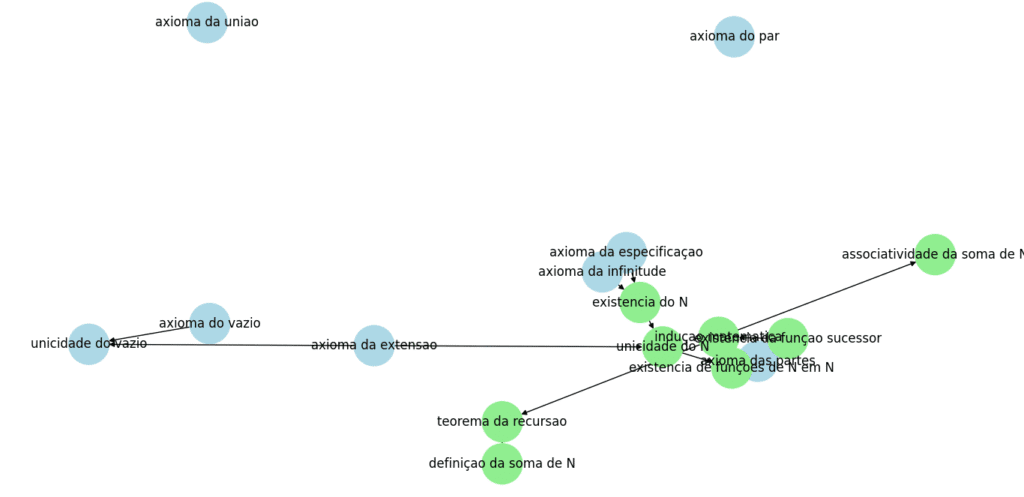
e essa é a parte embolada:
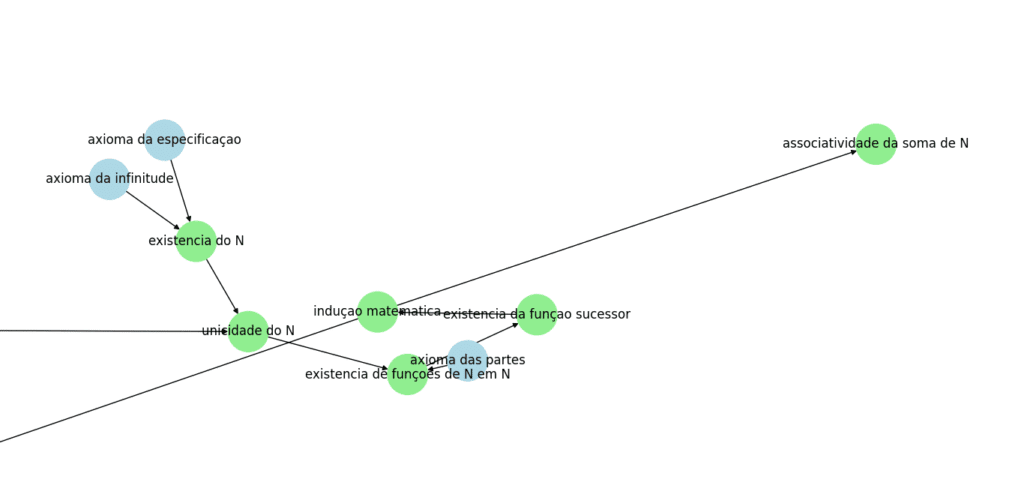
Apesar de já ter começado sinto que ele não está bom. Preciso aprender mais sobre as sentenças escritas no ZFC para continuar fazendo esse grafo. Um problema grande está sendo lidar com os teoremas de unicidade e as provas por indução, pois eu teria que ligar o axioma da extensão a todos os teoremas do primeiro tipo e o princípio da indução a todas as provas do segundo tipo. Não parece certo.
Acho que o meu grafo da matemática precisa ser conexo. Não sei se ele é planar e não sei se ele é k-colorível. Provavelmente os vértices que terão os maiores graus são o axioma da especificação e da extensão.
— publicidade —

