Introdução
Há um tempo atrás, eu assisti um shorts no youtube que te ensina a calcular uma aproximação para qualquer raiz quadrada não exata. Veja-o:
Meu objetivo nesse post é deduzir a fórmula dada no shorts.
Infelizmente usarei conceitos de Cálculo 1 na dedução que farei. Então você não entenderá a dedução se não estudou cálculo ainda :/
Mesmo nesse caso, sugiro que siga lendo até as coisas ficarem confusas. Na pior das hipóteses pule pro exemplo, que é apenas eu usando a fórmula do vídeo.
Sumário
— publicidade —
Pré-requisitos da geometria analítica
A dedução que vamos fazer é na verdade a aproximação linear da função $f(x) = \sqrt{x}$. Não se assuste com o nome pois a ideia é bem simples, como você verá a seguir.
Primeiramente, sabemos que o gráfico da função $f(x) = \sqrt{x}$ é:
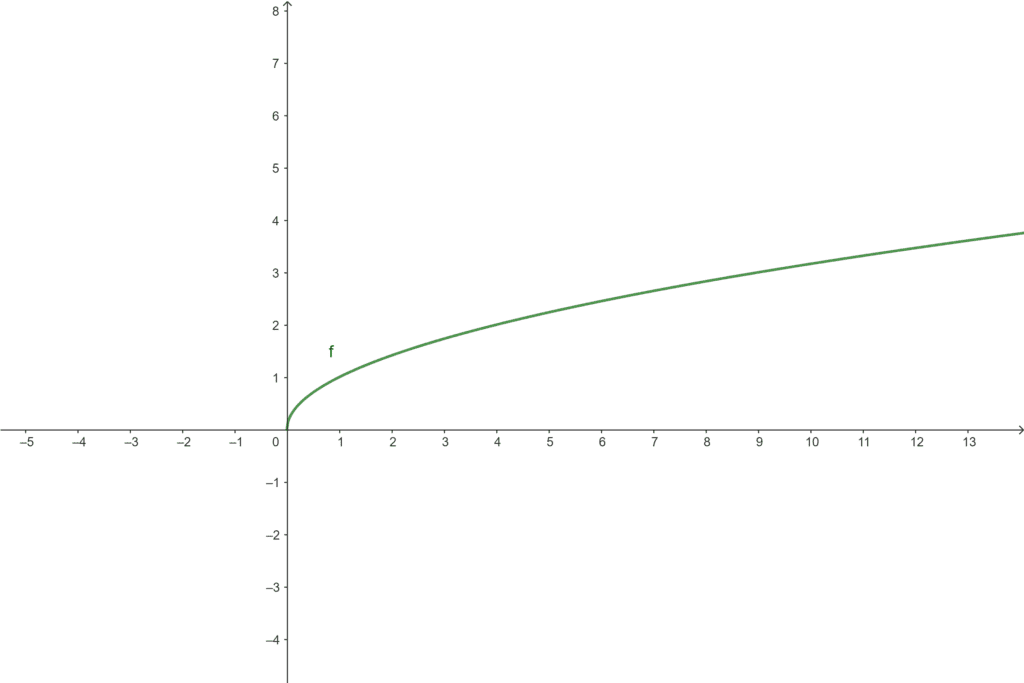
Calcular a raiz quadrada de um número $a$ é o mesmo que encontrar a ordenada do ponto $(a, f(a))$, que pertence ao gráfico de $f$:
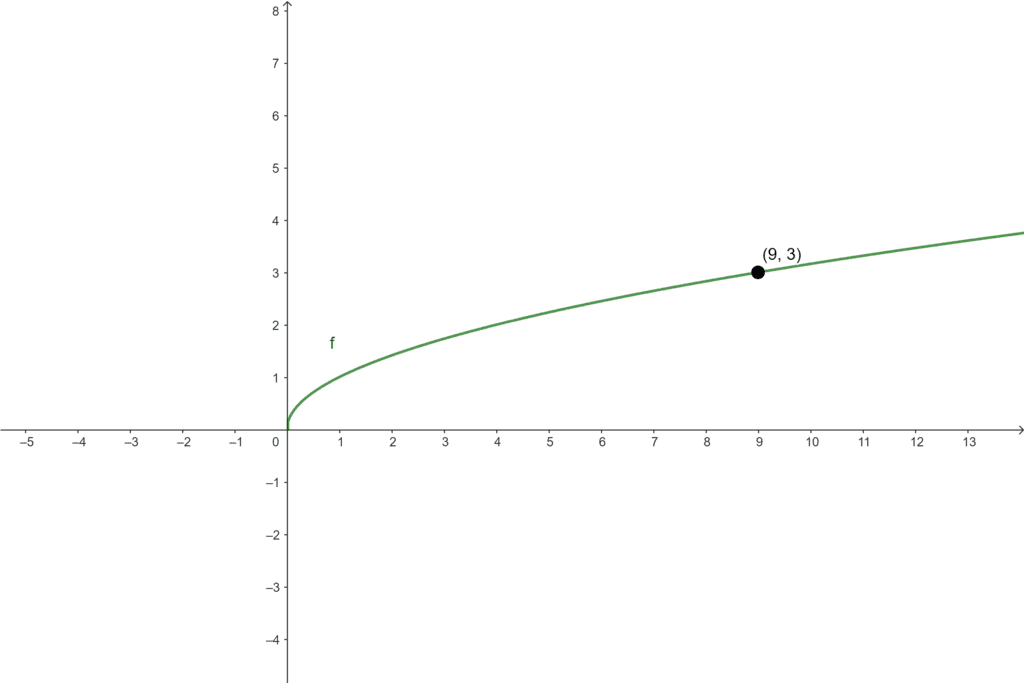
Portanto, saberemos calcular a raiz quadrada de qualquer número real se conseguirmos calcular a ordenada de qualquer ponto no gráfico de $f$.
Agora que transferimos nosso problema para a geometria analítica, usaremos o cálculo.
Pré-requisitos do cálculo
Com as técnicas do cálculo, conseguimos obter uma fórmula que nos dá os coeficientes angulares de todas as retas tangentes à função $f(x) = \sqrt{x}$, isso é justamente o que chamamos de derivada de $f$.
Se soubermos as coordenadas dos pontos de tangência (que pertencem tanto à reta quanto a função), poderemos unir essa informação com os coeficientes angulares e descobrir as equações de todas as retas tangentes a $f$.
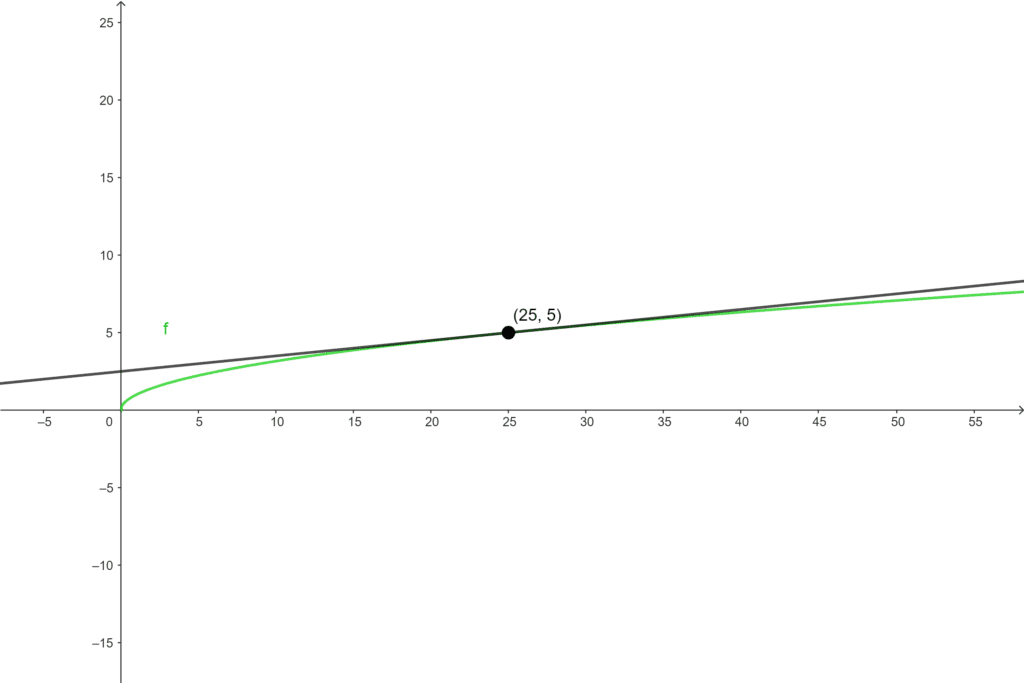
O problema é que num ponto em que a abscissa não é um quadrado perfeito, teríamos que calcular uma raiz quadrada não exata para descobrir sua ordenada. E como a derivada da nossa $f$ é $f'(x) = \frac{1}{2\sqrt{x}}$, teríamos que calcular a mesma raiz quadrada não exata para descobrir o coeficiente angular da reta tangente ao ponto.
Mas caso a abscissa do ponto seja um quadrado perfeito, conseguimos descobrir a equação da reta tangente a esse ponto sem ter que calcular nenhuma raiz quadrada não exata.
Dito isso, a pergunta natural que surge é: “isso nos ajuda em algo?” E a resposta é sim.
Dedução
Perto do ponto de tangência, as retas tangentes se parecem bastante com a função. Então ao invés de calcular diretamente a ordenada do ponto $(x, f(x))$, podemos usar a equação da reta tangente a um “ponto quadrado perfeito” próximo de $x$ e então calcular a ordenada do ponto que tem a mesma abscissa mas que se encontra na reta tangente.
Por exemplo, ao invés de calcular a ordenada do ponto $(26, \sqrt{26})$, podemos calcular a reta tangente ao ponto $(25, 5)$ e então calcular a imagem de $26$ na reta tangente, e não no gráfico da função.
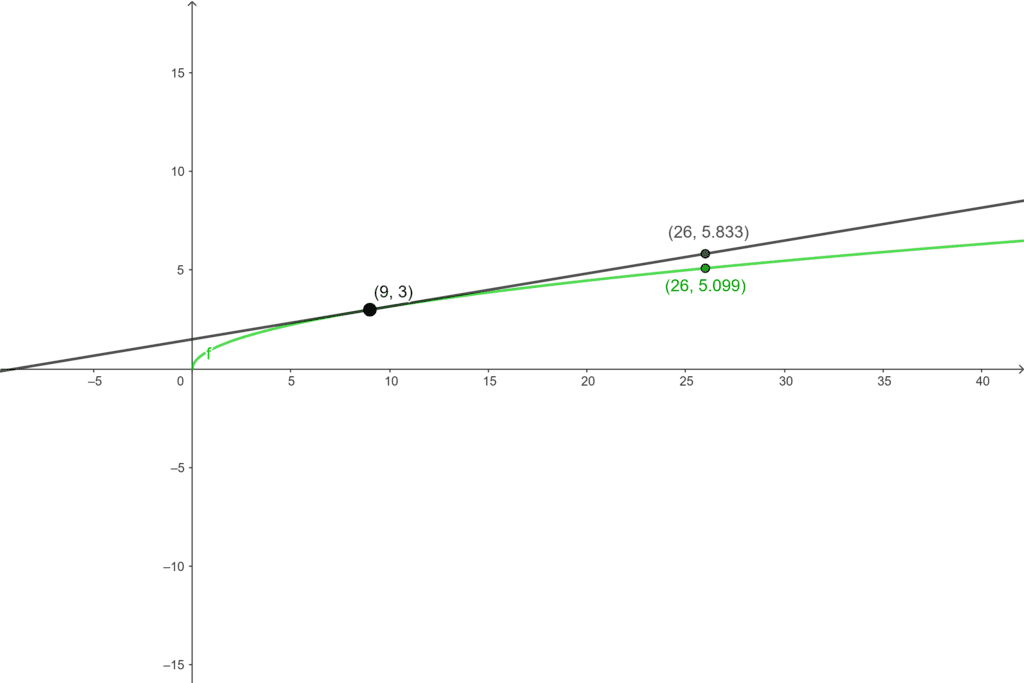
Então saber calcular a reta tangente a pontos específicos nos dá uma forma de calcular aproximações de todas as ordenadas dos pontos de $f$, sendo que quanto mais próximo o ponto específico tiver do ponto que queremos calcular a ordenada, melhor a aproximação.
Você verá que a dedução que farei a seguir consiste em calcular a imagem de todo número real na reta tangente que sabemos calcular mais próxima. É exatamente isso que chamamos de aproximação pela reta tangente de $f$ em um ponto (ou aproximação linear de $f$ em um ponto).
A partir daqui farei contas com esses conceitos, então o post ficará ainda mais difícil para aqueles sem conhecimentos de cálculo.
Dedução “formal”:
Seja $f: \mathbb{R}^+ \to \mathbb{R}$ tal que $f(x) = \sqrt{x}$ e seja $a \in \mathbb{R}^+$ o número que queremos calcular a raiz quadrada.
Seja $QP \in \mathbb{R}^+$ o quadrado perfeito mais próximo de $a$. Como a derivada de $f$ é $f'(x) = \frac{1}{2\sqrt{x}}$, temos que a reta tangente ao ponto $(QP, \sqrt{QP})$ tem a seguinte equação:
$$ y – \sqrt{QP}= \frac{1}{2\sqrt{QP}}(x – QP) $$
Chamamos essa equação de linearização de $f(x) = \sqrt{x}$ em $QP$.
Por tudo o que foi dito, se calcularmos a imagem de $a$ nessa reta, teremos uma aproximação de $\sqrt{a}$. Logo:
$$ \sqrt{a} – \sqrt{QP} \approx \frac{1}{2\sqrt{QP}}(a – QP) $$
Isolando $\sqrt{a}$ nessa “equação” obteremos:
$$ \sqrt{a} \approx \frac{a + QP}{2 \sqrt{QP}} \blacksquare$$
Essa é a aproximação linear de $f(x) = \sqrt{x}$ em $QP$. E também é a fórmula do shorts que queriamos deduzir!
Exemplo
Agora que deduzimos a fórmula, para calcular a aproximação de uma raiz quadrada não exata, basta literalmente só usá-la xD
Não há nenhum segredo nisso, o que farei é quase o mesmo que o professor do vídeo fez, com a diferença de que calcularei uma aproximação para $\sqrt{26}$ e não $\sqrt{23}$.
A fórmula é:
$$ \sqrt{a} \approx \frac{a + QP}{2 \sqrt{QP}} $$
Onde $a$ é o número que você quer descobrir a raiz e $QP$ o quadrado perfeito mais próximo de $a$.
Como o quadrado perfeito mais próximo de $26$ é $25$, temos que:
$$ \sqrt{26} \approx \frac{26 + 25}{2 \cdot \sqrt{25}} = \frac{51}{10} = 5,1 $$
A resposta “exata” de $\sqrt{26}$ é: $5,0990195135927848300282241090228…$
Diário de estudos
Generalização dessas ideias
O motivo de eu ter escrito esse post é que atualmente estou fazendo Cálculo 3, e uma das coisas que tive que estudar foi aproximações lineares de funções de duas variáveis. A ideia é a mesma, só que ao invés de retas tangentes e curvas, trabalhamos com planos tangentes e superfícies.
Mas, apesar da ideia ser a mesma, aumentar uma variável faz tudo ficar muito mais confuso, e é por isso que optei por escrever sobre funções de uma variável. Eu mesmo sinto que não venho aprendendo quase nada em Cálculo 3 justamente por causa da complexidade do curso (assim como em todos os outros ;-;)
Dúvidas sobre o tema
Para finalizar, quero comentar sobre duas dúvidas que tive enquanto escrevia esse post. Uma delas eu já tenho a resposta (mas é muito interessante) e a outra não.
A que eu tenho a resposta é: por que as aproximações que obtemos são sempre maiores que o valor real?
Caso não tenha notado isso, sugiro fazer alguns exemplos para se convencer de que isso é verdade.
Caso queira entender porque isso acontece, a resposta é que as retas tangentes sempre estão acima do gráfico da função raiz quadrada. Mas não acho que isso seja verdade para aproximações lineares de qualquer função.
A dúvida que eu não tenho resposta é: uma equação possui infinitos lugares geometricos?
Pergunto isso pois, se estivermos no $\mathbb{R}^3$, o lugar geométrico de $y = \sqrt{x}$ não é o que vimos aqui. Na verdade, ele seria o conjunto dos pontos da forma $(x, \sqrt{x}, z)$, onde $z$ pode ser qualquer número real. Isso dá a seguinte superfície:

Quer dizer que o lugar geométrico de uma equação depende do “ambiente” em que estamos? Isso é muuuito estranho.
Referências
Cálculo (Volume 1, 7ª edição) – James Stewart. O Stewart explica tudo que eu disse nesse post na página 226.
Obrigado por chegar até aqui ^^
Caso tenha gostado, leia meu outro post:
Dedução da soma dos termos de PG’s finitas e infinitas – Quarto 707
— publicidade —

