Recentemente descobri que o Google recomendou meu blog para algumas pessoas que pesquisaram “integral de seno ao quadrado”, e por isso resolvi fazer esse post. Essa recomendação provavelmente vem do fato de que eu já calculei essa integral no seguinte post:
Dedução da área do círculo usando integral – Quarto 707
Mas nada me impede de calcular de novo, explicando cada passo das contas.
Esse post será bem curtinho pois as contas não são tão complicadas, desde que usemos alguns conhecimentos prévios que falarei sobre.
Alternarei entre as notações $\frac{df(x)}{dx}$ e $f'(x)$ para expressar a derivada da função $f(x)$.
Conteúdo do post
— publicidade —
Conhecimentos prévios necessários
Para calcular a integral de seno ao quadrado, precisamos usar uma técnica de integração chamada integração por partes.
A integração por partes é um teorema que diz que:
\[ \int f'(x)g(x) \, dx = f(x)g(x)-\int g'(x)f(x) \, dx \]
Caso você não saiba por que isso é verdade, tente integrar os dois lados da regra do produto para derivadas e veja o que acontece.
Além da integração por partes, usaremos que “a derivada do seno é o cosseno e a derivada do cosseno é o menos seno”. Isto é:
\[ \frac{d\sin(x)}{dx} = \cos(x) \]
e
\[ \frac{d\cos(x)}{dx} = -\sin(x) \]
Mas a derivada de baixo usaremos na seguinte forma equivalente:
\[ \frac{d(-\cos(x))}{dx} = \sin(x) \]
Além disso, também usaremos que $\sin^2(x) + \cos^2(x) = 1$. Logo, $\cos^2(x) = 1-\sin^2(x)$.
Essa identidade pode ser deduzida usando o Teorema de Pitágoras num triângulo retângulo que tem hipotenusa de tamanho 1.
Por fim, usaremos o Teorema Fundamental do Cálculo, que diz que derivação e integração são operações inversas, no sentido de que a derivada de uma primitiva devolve a função original.
Cálculo da integral de sin²(x)
Tendo estabelecido os conhecimentos prévios necessários, bora fazer contas!
Primeiro precisamos reescrever a integral de seno ao quadrado da seguinte forma:
\[ \int \sin^2(x) \, dx = \int \sin(x) \cdot \sin(x) \, dx \]
Note que agora a integral procurada está numa forma em que podemos usar a integração por partes, onde nesse caso $f'(x) = \sin(x)$ e $g(x) = \sin(x)$.
Como $f'(x) = \sin(x)$, temos que $f(x) = -\cos(x)$.
E como $g(x) = \sin(x)$ temos que $g'(x) = \cos(x)$.
Usando a integração por partes, obtemos que
\[ \begin{align*} \int \sin(x) \cdot \sin(x) \, dx & = -\cos(x)\sin(x)-\int \cos(x)( -\cos(x)) \, dx \\ & = -\cos(x)\sin(x)+\int \cos^2(x) \, dx \end{align*} \]
E como $\cos^2(x) = 1-\sin^2(x)$, temos que:
\[ \begin{align*} \int \cos^2(x) \, dx & = \int 1-\sin^2(x) \, dx \\ & = \int 1 \, dx-\int \sin^2(x) \, dx \\ & = x-\int \sin^2(x) \, dx \end{align*} \]
(esqueci de falar que também usamos que a integral da soma é a soma das integrais e que a integral de $1$ é $x$ xD)
Resumindo tudo, o que descobrimos até agora é que:
\[ \int \sin^2(x) \, dx = -\cos(x)\sin(x)+x-\int \sin^2(x) \, dx \]
Daí, passando o $- \int \sin^2(x) \, dx$ pro lado esquerdo obtemos que:
\[ 2 \int \sin^2(x) \, dx = -\cos(x)\sin(x)+x \]
Portanto,
\[ \int \sin^2(x) \, dx = \frac{-\cos(x)\sin(x)+x}{2}+C \]
E ai está o resultado da integral!
Gráfico do resultado
Agora que calculamos a integral de seno ao quadrado, é interessante ver como é o gráfico do resutado, só por curiosidade mesmo:
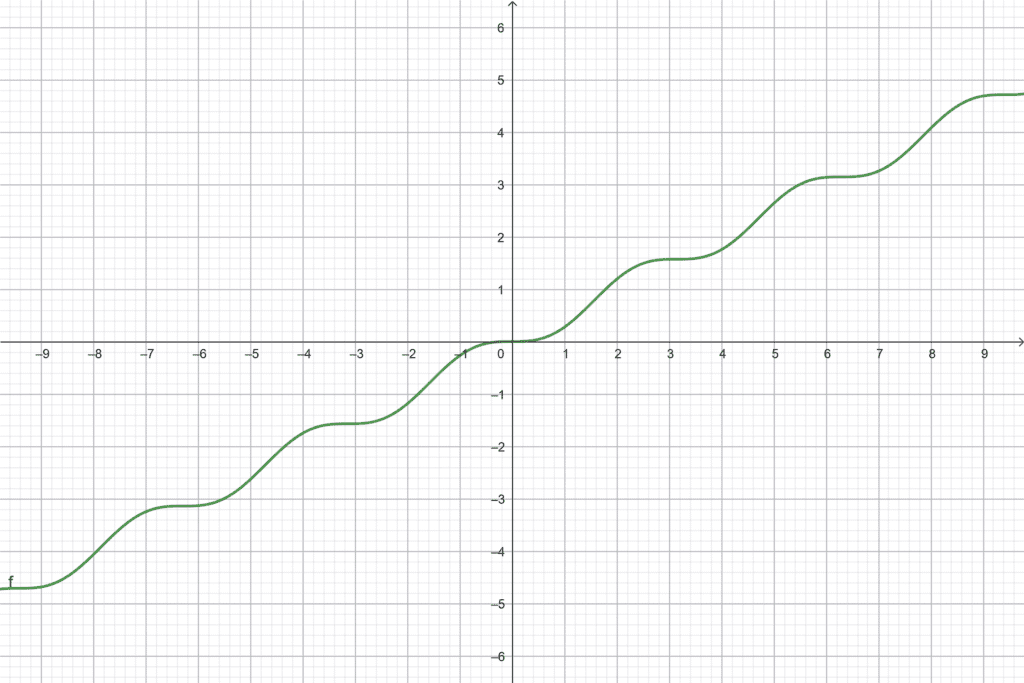
Bem bonitinho, não?
Comentários
Admito que não é nada trivial tentar deduzir a integral de seno ao quadrado se você nunca viu a dedução antes. Mas garanto que depois de ver você nunca esquece. Também dá pra calcular essa integral usando a fórmula do o arco duplo, mas usar integração por partes é mais fácil pra mim, pois não sei a fórmula do arco duplo de cabeça.
O curioso dessa dedução é que a integral reaparece no final da conta, permitindo que calculemos seu resultado resolvendo uma pequena equação algébrica. Esse tipo de “auto-referência” aparece em várias integrais interessantes que calculamos usando integração por partes. A razão disso é que a derivada do seno é o cosseno, e vice-versa (a menos de sinal). Isso faz com que, após usarmos a integração por partes apareça novamente a integral original.
Outra coisa curiosa é que essa integral aparece quando tentamos deduzir a área do círculo.
Obrigado por chegar até aqui ^^
— publicidade —

