Atualmente estou fazendo o curso Variáveis Complexas na graduação, e meu professor passou um exercício em que eu tinha que calcular a soma de uma PG específica, onde os termos da PG eram números complexos. Esse foi o estopim para eu começar esse post, pois isso é conteúdo que ele assumiu que eu já sabia e eu não sabia.
Ainda bem que ele é um bom professor, e quando pedi para que ele fizesse o exercício numa aula, ele foi a primeira pessoa a me explicar o que farei nesse post.
O que farei é a dedução da soma dos termos de uma PG (complexa ou não). Farei a dedução para PG’s finitas e infinitas.
Além disso, também comentarei um pouquinho sobre séries.
— publicidade —
Dedução da soma dos termos de uma PG finita
Seja $\{a_n\}$ uma sequência finita que também é uma progressão geométrica. Vou denotar a soma dos termos dessa PG como $S_n$.
Isso significa que:
$$ S_n = a_1+a_2+…+a_i+…+a_n $$
onde $a_i$ é o i-ésimo termo da PG.
Por se tratar de uma PG, temos que $a_n = a_i \cdot q^{n-i}$, onde $q$ é a razão da PG.
(caso essa segunda igualdade não esteja clara para você, há uma explicação/dedução dela no livro Noções de Matemática – Volume 2)
Na primeira igualdade, podemos colocar uma razão em evidência e obter:
$$ S_n = a_1+q(a_1+…+a_{n-1}) $$
Notando que $a_1+… +a_{n-1} = S_n-a_n$, teremos que:
$$ S_n = a_1+q(S_n-a_n) $$
Supondo que $q \neq 1$ e isolando $S_n$, teremos finalmente que:
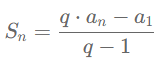
(faça as contas sozinho(a)!!)
E aí está a dedução da soma dos termos de qualquer PG finita. Mas se quisermos $S_n$ em termos apenas de $a_1$ e $q$, precisamos reparar que $q \cdot a_n = q \cdot a_1 \cdot q^{n-1} = a_1 \cdot q^n$. Logo, podemos reescrever a equação acima como:
$$ S_n = \frac{a_1(q^n-1)}{q-1} $$
(o meu professor deduziu essa fórmula de um jeito um pouco diferente do que eu fiz, mas a essência é a mesma)
No caso em que $q = 1$, vemos que o que fizemos não pode ser feito pois estaríamos fazendo uma divisão por zero. Por sorte, é fácil de deduzir $S_n$ quando $q = 1$. $S_n$ será $n \cdot a_1$, pois estaríamos somando $a_1$ n vezes.
Dedução da soma dos termos de uma PG infinita
Agora vejamos o que acontece quando a PG é infinita, isto é, possui infinitas parcelas.
Caso você ainda não tenha estudado cálculo, recomendo que pare de ler por aqui (ou talvez não, porque não tratarei o problema com rigor).
Se $|q| > 1$, os termos dessa PG infinita cresceriam em módulo à medida em que $n$ aumenta, logo a soma tenderia para o infinito. No entanto, se $|q| < 1$, os termos da PG se aproximam de $0$ à medida que $n$ aumenta, e portanto o termo $a_n$ tende a $0$. É de se esperar então que a soma infinita (ou série) também se aproxime indefinidamente de algum valor, já que a partir de algum $a_i$ estaríamos somando parcelas minúsculas!
Analisemos isso com mais detalhes.
Supondo $|q| < 1$, se usarmos o conceito/notação de limite que vemos em Cálculo, o que eu disse acima sobre $a_n$ pode ser simbolizado da seguinte forma:
$$ \lim_{n\to\infty} a_n = 0 $$
Usando o que deduzimos, temos que a soma dos $n$ primeiros termos dessa PG infinita será:
$$ S_n = \frac{q \cdot a_n-a_1}{q-1} $$
Se fizermos $n$ tender ao infinito dos dois lados da equação temos que:
$$ \lim_{n\to\infty} S_n = \lim_{n\to\infty} \frac{a_n \cdot q-a_1}{q-1} $$
Usando algumas propriedades de limites, podemos escrever a soma que procuramos da seguinte forma:
$ \lim_{n\to\infty} S_n = \frac{\lim_{n\to\infty} (a_n \cdot q) – \lim_{n\to\infty} a_1}{\lim_{n\to\infty} (q-1)} $
Usando a continuidade das funções constantes, obteremos:
$$ \lim_{n\to\infty} S_n = \frac{\lim_{n\to\infty} (a_n \cdot q)-a_1}{q-1} $$
Como $\lim_{n\to\infty} a_n = 0$, concluímos que:
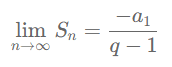
E aí está a dedução da soma dos termos de uma PG infinita!
Dúvidas e conclusões desse estudo
Dúvidas
Minha primeira dúvida é se algum matemático chamaria essas contas que fiz de demonstração. Eu acho que não, pois creio que para isso precisaríamos usar indução matemática ou outras coisas sofisticadas.
Minha segunda dúvida é sobre o que acontece caso tentemos deduzir a soma dos termos de uma PG infinita da mesma forma que deduzimos a de uma PG finita. Veja o que acontece:

Conclusões
Antes de finalizar, quero chamar a sua atenção para ver que o que fizemos nos dá um jeito de escrever infinitas funções como uma soma infinita!
Por exemplo:
Seja a PG infinita:
$$ x + \frac{x}{2} + \frac{x}{4} + \frac{x}{8} + … $$
onde $q = \frac{1}{2}$ e $a_1 = x$, com $x$ sendo uma variável.
Usando a fórmula da soma infinita, temos que a soma dos termos dessa PG é:
$$ \frac{-x}{\frac{1}{2}-1} = 2x $$
Logo, uma representação em série da função $f(x) = 2x$ é:
$ f(x) = 2x = x + \frac{x}{2} + \frac{x}{4} + \frac{x}{8} + … $
É possível descobrir a representação em série de infinitas funções dessa forma, basta ficar mudando $a_1$ ou $q$.
(aliás, todo lugar que vi fazia a variável $x$ da função ser $q$, e não $a_1$ como eu fiz acima. Obviamente eles encontravam a expansão em série de outras funções)
Acho que Newton foi o primeiro a escrever as funções como séries. E, graças a esse post, $f(x) = 2x$ foi a primeira função não constante que escrevi como série.
Diário de estudos
Eu deveria ter visto muito mais coisas sobre séries, pois está na ementa de Cálculo 2, só que não tive isso quando fiz essa matéria. Mas não faz tanta diferença assim pois não costumo aprender muito do que vejo na graduação.
Eu até vi um pouco de séries em Variáveis Complexas e Cálculo 4, mas não entendi nada. (os profs deram mais por curiosidade mesmo, eles não botaram na prova). Aparentemente poder representar uma função como uma soma infinita é importante pra deduzir a fórmula de Euler e pro teorema de existência e unicidade de equações diferenciais de primeira ordem.
De qualquer forma, sei que verei essas coisas quando eu fizer Análise 1. Só espero conseguir aprender alguma coisa lá.
Caso tenha curiosidade, o exercício que meu professor de Variáveis Complexas passou que me fez escrever esse post é:
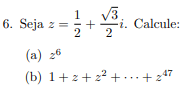
(é necessário também usar a fórmula de The Moivre nesse exercício)
Referências
Noções de Matemática – Volume 2 -> Ele deduz a fórmula do termo geral de uma PG na página 109 e faz tudo o que fiz nesse post nas páginas 126 a 132.
Stewart – Volume 2 (6ª edição) -> Na página 692 o Stewart acha a representação em série da função $f(x) = \frac{1}{1 – x}$ usando o que foi feito aqui.
— publicidade —

