3 deduções da derivada da função exponencial

Atualmente estou fazendo Cálculo 2 na faculdade, e ai naturalmente me veio a dúvida: qual é a derivada da função exponencial?

Esta é uma dúvida de Cálculo 1 que eu venho negligenciando desde que fiz esse curso. Mas finalmente tomei vergonha na cara para responde-la e e para guardar minha resposta nesse diário de estudos!

Abaixo está a tabela de conteúdos deste estudo que fiz:

Tabela de conteúdos

Primeiras Impressões
Deduções da derivada da função exponencial
Isso são demonstrações?
Pesquisa como um trabalho em equipe
Dúvidas que surgiram enquanto eu estudava isso
Referências

Primeiras Impressões

Quando a base da função exponencial é o número de Euler $e$ , minha mente diz rapidamente: “a derivada de $e^x$ é $e^x$ !”. Mas eu não decorei a resposta para uma base qualquer.

Aí, pra tentar descobrir a derivada de uma função exponencial com uma base $a$ qualquer, eu tentei usar a definição de derivada (em termos de limites). Ou seja, meu ponto de partida foi a seguinte igualdade:

$\frac{\mathrm{d}a^x}{\mathrm{d}x} = \lim\limits_{h \to 0} \frac{a^{x+h} - a^x}{h}$

Daí eu brinquei um pouco com essa expressão da seguinte forma:

Desenvolvimento da definição (em termos de limites) da derivada da função exponencial.

O problema é que apareceu um outro limite que eu também não sabia resolver, então fui ler o Stewart pra ver se ele me dava alguma luz e descobri que ele fez as exatas mesmas contas!

Além das contas, ele fez uma observação importante sobre esse limite que apareceu. Veja:

As mesmas contas da foto de cima, mas feitas no livro do Stewart.

Continuação + comentário das contas no livro do Stewart. — fiquei muito feliz quando vi que as contas que fiz tem valor o suficiente para estarem num livro

Note que o Stewart “calcula” numericamente o limite que apareceu quando $a = 2$ ou $a = 3$ , e diz que existe um valor que o $a$ pode assumir que faz o limite que apareceu ser igual a 1. Aí ele define esse valor como sendo o $e$ (sem nem mesmo provar que esse valor é único).

(E é bem estranho o fato do Stewart usar o $e$ para definir o próprio $e$ )

Maaas… apesar de tudo isso ser muito interessante ~~e um pouco confuso~~, o Stewart não resolveu o limite que eu precisava para deduzir a derivada de uma função exponencial qualquer.

Deduções da derivada da função exponencial

Dedução por l’Hôpital

Então ~~graças a incompetência do Stewart~~ eu pedi ajuda a 2 amigos meus. Um deles me deu uma resposta imediatamente após eu perguntar, e eu só fiquei pensando em como ~~esse disgramado~~ conseguiu. Aí ele me falou que fez de cabeça usando l’Hôpital.

Eu nunca resolvi um limite usando isso, então não vou colocar a dedução detalhada aqui, mas considere essa como sendo uma das 3 soluções prometidas no título.

(se eu colocasse só ‘duas deduções’ no título, ele não ficaria tão imponente xD)

Dedução natural

Meu outro amigo resolveu o limite que apareceu na marra, e me mandou essa resposta (com um atraso de uns 2 dias):

Foto que o meu amigo me mandou resolvendo o limite que apareceu no desenvolvimento da definição (em termos de limites) da derivada da função exponencial. — eu até poderia escrever essas contas pra não ter que usar essa imagem horrível, mas acho que usando ela o texto fica com mais cara de diário

Note que agora é possível terminar a dedução da derivada de uma função exponencial qualquer, incorporando essas contas que meu amigo me mandou nas contas iniciais (que estão nessa foto).

O resultado é:

Dedução final da derivada de uma função exponencial qualquer.

E essa é a nossa segunda dedução da derivada da função exponencial! Ela é deveras estranha porque usa uma substituição de variáveis e uma definição do $e$ diferente da do Stewart. Mas essa é sem dúvidas a solução mais natural, pois é simplesmente o cálculo do limite que é literalmente a definição da derivada da função exponencial.

Essa solução é tão natural que eu comecei a atacar o problema justamente fazendo o começo dessas contas.

Dedução usando a regra da cadeia

O curioso é que essas contas não estão no Stewart, e eu cheguei a achar que o livro não deduzia a derivada de uma função exponencial qualquer.

Mas na verdade ele deduz sim. Só que ele só faz isso depois de explicar a regra da cadeia. (20 páginas depois dessas)

E a razão disso é que ele não faz a dedução calculando o limite como fizemos, e sim usando a regra da cadeia e uma sacada genial.

A sacada é usar a identidade:

$a^x = e^{\ln(a^x)}$

Ela é genial porque o lado direito da igualdade é uma função composta, então agora o Stewart encara $a^x$ como uma função composta, e usa a regra da cadeia para descobrir sua derivada da seguinte forma:

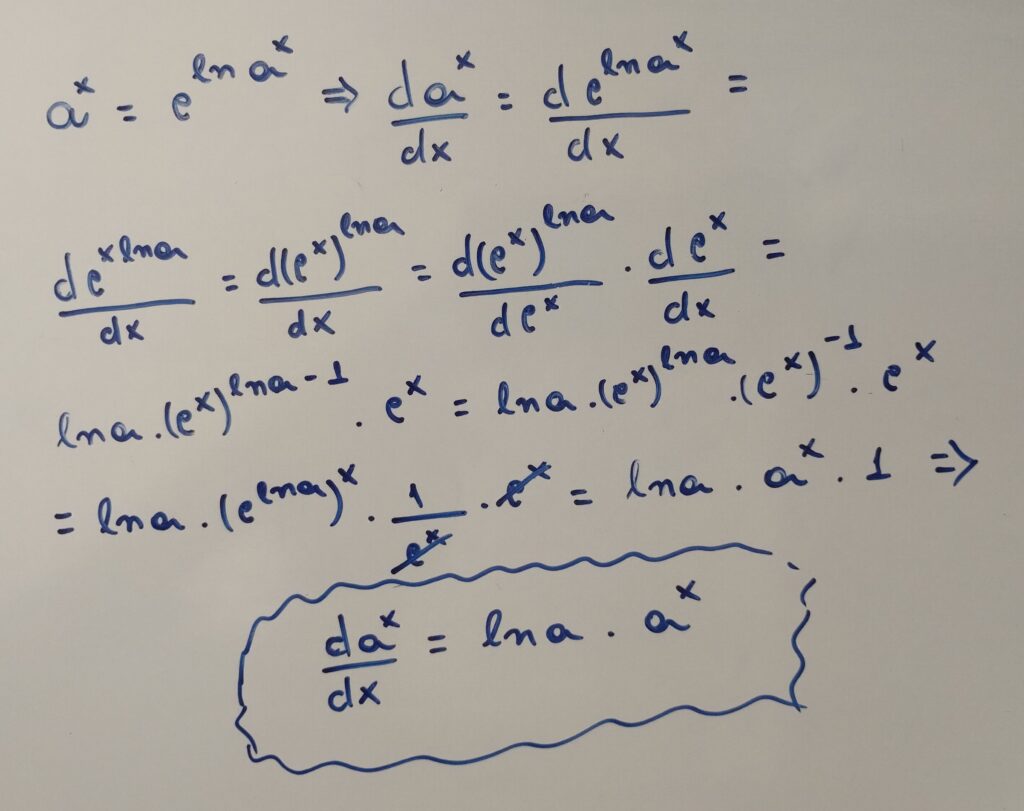
Dedução da derivada de uma função exponencial qualquer usando a regra da cadeia.

Caso você queira ver as contas direto da fonte:

A mesma dedução usando a regra da cadeia, só que no livro do Stewart.

E essa é a nossa terceira (e última) dedução da derivada da função exponencial para uma base qualquer.

Caso você queira ver uma quarta dedução (que usa derivação implicita), tem nesse site: Derivadas das funções exponenciais – Só Matemática.

Isso são demonstrações?

Finalmente, ai estão as 3 deduções prometidas.

Note que eu não usei a palavra demonstração em momento nenhum, apesar do texto permitir (eu acho).

Tomei essa decisão porque, assim como Frege no início de sua pesquisa, eu não sei o que é uma demonstração.

Mas, o que importa é que eu acho que sei o que é uma dedução: um raciocínio que você explicita para chegar em uma conclusão que você não sabe ou esqueceu.

(E essas deduções do texto são exatamente isso para mim!)

Como um estudante de matemática, meus professores esperam que eu saiba de cabeça qual é a derivada de $a^x$ , para usar isso em contas mais complicadas como por exemplo calcular a derivada da função:

$f(x) = a^x \sin(e^x)$

Mas como eu não quero decorar a resposta, acabo não sabendo de cabeça.

(Apesar de que eu mostrei esse texto para um professor meu e ele disse que não espera isso dos seus alunos, porque nem ele mesmo sabe a derivada de $a^x$ de cabeça. Mas esse professor é um querido e não acho que ele sirva como parâmetro pros outros)

De qualquer forma, o que importa é que agora sempre que eu esquecer esse resultado, eu posso refazer alguma dessas deduções no canto da folha para relembrar o resultado.

(Provavelmente a por L’Hospital seria a mais eficiente. Tenho que aprender isso logo ;-;)

Ou seja, eu posso deduzir essa informação sempre que eu precisar, sem precisar decorar a resposta. Só terei que decorar as deduções. Mas isso é mais fácil que decorar a resposta por ser mais natural.

Pesquisa como um trabalho em equipe

Dito isso tudo, eu também queria falar um pouquinho sobre como estudar.

Note que ao me deparar com um problema, eu tentei resolve-lo sozinho, mas na primeira dificuldade eu pedi ajuda aos meus amigos.

Fiz isso porque ultimamente tenho achado que ver a resposta de alguém (depois de tentando fazer sozinho) também é importante no processo de aprendizagem.

Talvez a razão de eu estar pensando assim seja um conselho que recebi esse semestre de um professor meu que leu a versão beta desse post.

Ele me disse que a matemática é inabarcável, e que fazer pesquisa na matemática é muito mais sobre trabalho em equipe do que sobre acumular conhecimento, justamente porque é impossível conhecer tudo da matemática.

E o que eu entendo por trabalho em equipe é compartilhar conhecimento, então pedi aos meus amigos para compartilharem os seus conhecimentos comigo.

Apesar do meu professor ter falado sobre pesquisa, a graduação também é (de certa forma) uma pesquisa, só que de assuntos mais fáceis. Então é interessante que eu trabalhe em equipe na graduação também.

Foi por isso que não me importei em pedir ajuda.

~~(Já que tenho amigos inteligentes, porque não usá-los para alguma coisa? hehe)~~

Dúvidas que surgiram enquanto eu estudava isso

Por fim, como de costume nos posts que são diários de estudo, falarei das dúvidas que tive enquanto escrevia esse texto.

Dúvidas tranquilas

Uma dúvida que tive é sobre a definição do $e$ . Note que o meu amigo e o Stewart usaram definições diferentes do $e$ . Mas ambos usaram a ideia de limite nelas. Talvez renda bons frutos eu pesquisar mais sobre o $e$ .

Além disso, outra dúvida que ressurgiu foi o que é uma substituição de variáveis. Meu amigo usou uma substituição para resolver o limite que eu não consegui, e eu não sei o que é isso.

No começo desse semestre eu até perguntei o que é uma substituição de variáveis para minha professora de Cálculo 2, e ela falou que é uma mudança no tamanho da unidade do seu sistema de coordenadas, seja lá o que isso signifique.

Dúvidas “incomodantes”

A dúvida que mais me assombrou enquanto eu estudava isso é: como caralhos eu devo interpretar essas contas?

Beleza que agora eu consigo deduzir a derivada de $a^x$ sempre que eu precisar… Mas o que o resultado significa?

Se eu pensar na derivada de uma função como sua taxa de variação, então uma forma de interpretar a resultado das contas é: a taxa de variação de uma função exponencial qualquer em um input qualquer é o $e$ elevado ao input vezes o log do input na base da função exponencial.

O problema é que essa frase é muito estranha.

Espero esclarecer essas coisas em algum momento da minha vida.

Por fim, meu professor também sugeriu uma outra dúvida, que é: o que é $\bold{a^x}$ quando x é irracional?

Parece um problema legal de se pensar, mas eu já não aguento mais problemas, então tô comentando só a título de curiosidade mesmo.

Muito obrigado por chegar até aqui :]

Caso você queira ver também uma dedução para a integral da função exponencial, acesse:

Dedução da integral da função exponencial – Quarto 707

Caso queira ver deduções para a derivada e a integral da inversa da função inversa a exponencial, acesse:

Dedução da derivada da função logaritmo – Quarto 707

Dedução da integral da função logaritmo – Quarto 707

Referências

Cálculo – James Stewart (7ª edição)